2022 IUPC가 무사히 개최되었고, 별 탈 없이 마무리 되었다.
이제 학교를 졸업해서 참여하기 매우 어려울 것이라고 생각했는데, 어떻게든 참가할 수 있었다!
오프라인으로 프로그래밍 대회를 개최하고 그 열기를 직접 느낄 수 있었다는 것에 메우 만족한다.
과연 내년에도 문제를 출제할 수 있을까? 1년 후에 공개됩니다!
문제 출제
이번에는 대회 준비를 처음부터 함께하지는 않았고 도중에 추가멤버로서 참가했다. 후보 문제들의 출제가 거의 끝난 상태였기 때문에, 그리고 그 문제들의 퀄리티가 정말 좋다고 느꼈기 때문에 출제 쪽에서 내가 더 할 일은 딱히 없었다.
대신 그 중 어떤 문제들을 출제할지에 대한 교통정리를 담당했다.
먼저 후보 문제들이 전체적으로 굉장히 코드포스나 앳코더 등의 온라인 프로그래밍 대회에서 나올법한 문제들이었기 때문에, 조금 더 전형적인 문제가 되도록 조금 수정하거나 직접 추가했다.
또 이번 대회가 팀전이 아닌 개인전으로 진행되었기 때문에 문제를 12문제에서 10문제로 줄이고, 문제들의 난이도의 중앙값이 실버 중상위 정도가 되도록 조정했다.
내가 출제한 문제들의 난이도가 낮았던 이유도 이 때문이다. (너의 학점은, 조각 케이크)
그렇게 10문제 출제를 확정짓고 나서 보니, 교내 대회로서는 좋은 문제 셋이었지만 고인물이 득실득실한 오픈컨테스트로서는 조금 심심하다는 느낌이 들었다. 추가로 Hard 두 문제를 추가한 이유이다.
그 두 문제에 대한 얘기는 후술한다.
그렇게 검수도 나쁘지 않게 진행되었고, 실제 오프라인 대회와 Open Contest까지 큰 문제없이 마칠 수 있었다.
오프라인 대회는 전날부터 (무려 연차를 쓰고) 준비했고, 물리적으로 몸이 힘들었다는 점만 빼면 당일 스코어보드와 코드들을 보며 재미있게 즐길 수 있었다.

다음은 각 문제들의 출제의도와 해설에 대해 간략하게 설명한다.
아, 참고로 문제 순서는 가나다순이다.
A. 경로당펑크 2077
https://www.acmicpc.net/problem/25205
25205번: 경로당펑크 2077
시은이는 종합설계 프로젝트로 오픈월드 액션 고스톱 게임 경로당펑크 2077을 개발하고 있다. 대사를 추가하던 중, 사용자 이름에 따라 '을' 또는 '를' 중 하나를 출력해야 함을 깨달았다. 예를 들
www.acmicpc.net
출석체크 문제였다.
자음이든 모음이든 한두개씩 빠트린 사람들의 고통받는 모습을 볼 수 있었다.
아래는 문제와 아마도 관련없는 노래이다.
B. 너의 평점은
https://www.acmicpc.net/problem/25206
25206번: 너의 평점은
인하대학교 컴퓨터공학과를 졸업하기 위해서는, 전공평점이 3.3 이상이거나 졸업고사를 통과해야 한다. 그런데 아뿔싸, 치훈이는 깜빡하고 졸업고사를 응시하지 않았다는 사실을 깨달았다! 치
www.acmicpc.net
* 본 문제는 실화를 바탕으로 제작되었습니다.
정수 실수 문자열을 다룰 수 있고, 반복문과 조건문을 사용할 수 있다면 충분히 맞을 수 있다.
참고로, 본인은 후에 열린 2차 졸업고사를 응시하여 합격 커트라인을 간당간당하게 넘어 간신히 졸업할 수 있었다.
C. 바벨탑의 저주
https://www.acmicpc.net/problem/25207
25207번: 바벨탑의 저주
바벨탑은 $N$개의 방이 $N$ - 1개의 통로로 연결된 이차원 건축물이다. 어떤 방들은 저주의 방으로, 접근하면 화를 입는다고 한다. 탑은 아래 그림과 같이 방과 통로가 각각 노드와 간선인 트리 그
www.acmicpc.net
풀지 말라고 낸 문제이다.
참가자들이 그림과 설명을 보고 무서워서 바로 다른 문제로 도망칠 줄 알았는데, 의외로 많은 사람들이 제출했다. 얼핏보면 단순 구현문제 같아보여서 그런걸까?
교내대회에서는 풀리지 않았고, 오픈 컨테스트에서 AC를 받은 답안은 대부분 트리를 잘 해싱해서 푸는 방법이었다.
물론 해싱을 굳이 막지는 않았지만 (막을 수도 없었지만), 조금 더 이쁜 방식으로 풀 수 있는 문제였다.
트리를 중위순회하여 방문한 노드들을 순서대로 쭉 써놓고 열심히 째려보면 다음과 같은 사실을 알 수 있다.
1. 각 서브트리는 연속된 구간으로 나타내어진다.
2. 서브트리를 뒤집어도 같아지려면, 이 구간이 팰린드롬이어야 한다.
따라서, 팰린드롬을 빠르게 판별할 수 있는 Manacher를 이용하여 문제를 풀 수 있다.
각 노드를 {쓰인 숫자, 깊이}의 pair로 저장하면 연속된 각 구간이 유일한 서브트리를 나타내게 된다.
D. 새벽의 탐정 게임
https://www.acmicpc.net/problem/25208
25208번: 새벽의 탐정 게임
새벽의 탐정 게임은 재미있는 2인용 보드게임이다. 한 명은 탐정, 다른 한 명은 도둑 역할을 맡는다. 게임은 $N$행 $M$열 격자 위에서 진행된다. 격자의 각 칸은 벽이 설치되어 있거나 비어있고, 역
www.acmicpc.net
감옥의 상태는 (행, 열, 뚫린 면의 위치) 총 3가지의 변수로 나타낼 수 있다.
결국 감옥의 시작 상태와 끝 상태 사이의 최단거리를 묻는 문제이고, 간선의 가중치가 모두 같으므로 BFS로 문제를 해결할 수 있다.
나머지는 감옥 굴리기를 열심히 구현하면 된다.
원래는 조금 더 신박한 문제였는데, 최단거리 요소를 가진 문제가 하나 있으면 좋을 것 같아 어딘가의 코딩테스트에서 나올 것 같이 생긴 문제로 바꾸게 되었다.
E. 샤카샤카
https://www.acmicpc.net/problem/25209
25209번: 샤카샤카
샤카샤카는 직사각형 보드 위에서 즐기는 퍼즐 게임이다. 보드는 N행 M열의 격자로 구분되어 있으며, 각 칸에 블록을 하나 놓을 수 있다. 퍼즐을 해결하려면 게임을 시작하기 전 주어지는
www.acmicpc.net
5시간이라는 시간은 누군가에게는 매우 긴 시간이다. 이미 풀만한 문제를 다 푼 사람들은 이 빡구현 문제를 풀면서 시간을 때울 수 있지 않을까? 라는 출제의도로 나온 문제이다.
보드의 크기가 최대 10 x 10이라서 어떤 이상한 시간복잡도가 와도 웬만하면 통과되었을 것이므로 어떻게든 구현만 잘 하면 되는 문제라 꽤 풀거라고 예상했는데, 보기 좋게 빗나가버렸다.
오픈 컨테스트에서도 단 5명만이 풀었고, 대회의 히든보스 문제가 되었다...
Hard 문제를 정할 때 샤카샤카 솔버를 만들도록 시킬까 조금 고민했었는데, 풀이가 생각나지 않았고, 그냥 또다른 더러운 구현 문제가 늘어날 것 같아 아쉽게도 샤카샤카 (Hard)는 나오지 않았다.
F. 정사각형 세기
https://www.acmicpc.net/problem/25210
25210번: 정사각형 세기
입력은 4줄로 주어진다. 각 줄에는 4개의 정수 x1, y1, x2, y2가 공백으로 구분되어 주어진다. i번째 줄에 주어진 (x1, y1)은 제 i사분면에 그린 직사각형의 꼭짓점 중
www.acmicpc.net
우선 각 직사각형의 상하좌우로 튀어나온 부분은 정사각형을 만드는데 쓸 수 없으므로 잘라낸다.
그 후 1사분면과 3사분면의 직사각형과 겹치도록, y=x+k꼴의 직선을 하나 그어보자.
1사분면 직사각형과 직선이 겹치는 점의 개수와 3사분면 직사각형과 직선이 겹치는 점의 개수를 곱하면 꼭지점 2개가 해당 직선 위에 있는 정사각형의 모든 경우의 수를 구할 수 있다.
이 때 가능한 직선의 경우의 수가 약 20만개 정도이므로, 이를 모두 더하면 답이 된다.
교육적인 문제라고 생각한다.
완전탐색으로 풀면 시간복잡도가 어떻게 되는지, 이를 O(N)까지 줄이려면 어떤 요소를 줄이고 없애야 하는지 생각하는 것이 중요한 문제였다.
하지만 출제자님이 한 가지 간과한 사실이 있었다.
F2. 정사각형 세기 (Hard)
https://www.acmicpc.net/problem/25211
25211번: 정사각형 세기 (Hard)
민겸이는 4개의 서로 다른 사분면 위에 각 변이 x축 또는 y축에 평행하면서 네 꼭짓점이 모두 격자점 위에 있는 직사각형을 하나씩 그렸다. 각 직사각형에서 x, y 좌표가 모두 정수인
www.acmicpc.net
바로 이 문제를 상수시간에도 풀 수 있다는 사실이었다.
직사각형의 튀어나온 부분을 잘라낸 다음, 1사분면과 3사분면 직사각형의 각 꼭지점을 지나도록 y=x+k꼴의 직선들을 긋자.
이웃한 두 직선 사이에 있는 부분에서 하나의 직사각형과 겹치는 점의 개수는 k에 대한 일차식으로 나타낼 수 있고, 이를 두 개 곱하므로 만들 수 있는 정사각형의 개수를 k에 대한 이차식으로 나타낼 수 있다.
이를 k에 적당한 수 a부터 b까지 넣었을 때의 합을 구하면 된다.
이 외에 포함배제를 이용한 풀이도 검수단계에서 볼 수 있었다.
G. 조각 케이크
https://www.acmicpc.net/problem/25212
25212번: 조각 케이크
조각 케이크들을 골랐을 때, 고른 조각 케이크를 모두 합쳐서 케이크 한 판으로 만들 수 있는 경우의 수를 출력한다.
www.acmicpc.net
작년 대회에서 쓰지 못한 후보 문제를 재활용 해왔다.

원래는 대충 이런 사진을 보고 분수 타일을 조합하는 문제였는데, 분수를 나타낼 수 있는 요소가 뭐가 있을까 하다가 조각 케이크를 생각해낼 수 있었다.
단순히 2n가지 모든 경우의 수를 탐색하면 된다.
n이 작기 때문에 유리수 구현은 필요 없고, C++ double 자료형으로도 충분히 AC를 맞을 수 있다.
G2. 조각 케이크 (Hard)
https://www.acmicpc.net/problem/25213
25213번: 조각 케이크 (Hard)
조각 케이크들을 골랐을 때, 고른 조각 케이크를 모두 합쳐서 케이크 한 판으로 만들 수 있는 경우의 수를 출력한다. 답이 매우 커질 수 있으므로, 109+7로 나눈 나머지를 출력한다.
www.acmicpc.net

Hard 문제를 뭘로 할 지 고민할 때, 이 문제에서 n이 커지면 풀 수 있을까 생각해봤다.
잘 생각해보니 될 것 같기도 해서 일단 문제로 만든 다음 구현을 해 보았다.
원래는 c가 최대 20이었고, map dp와 조합론을 섞어서 풀어야 하는 문제로 만들었는데 문제를 다듬던 중 큰 문제를 발견했다. 생각보다 겹치는 부분문제가 적어서, dp가 필요없다는 사실이었다!
실제로도 그냥 완전탐색에 조합론만 섞어 풀어도 dp풀이와 시간차이가 거의 없었다.
이와 별개로 굉장히 빠른 MITM 풀이를 발견했고, 이를 별해로 하려고 했지만 단순히 조합론만으로 풀리는 건 원하지 않았기 때문에 c의 범위를 늘리기로 했다.
맨 처음에는 c를 40정도 늘릴 생각이었는데 너무 경우의 수가 많아서 제한 시간안에 풀 수가 없었고, 실험을 거듭해서 25라는 적절한 수치를 찾을 수 있었다.
이에 맞춰 Easy버전도 c를 25까지 늘려서 데이터를 새로 만들었다. 실수 풀이가 틀릴까 걱정을 많이 했는데, 다행히 double풀이가 멀쩡한 것을 보고 안심할 수 있었다.
아무튼 그래서 MITM으로 풀 수 있다.
단순히 케이크의 종류를 1~12 / 13~25 와 같이 반으로 나누면 안되고, 최대한 나올 수 있는 경우의 수가 비슷하도록 (LCM이 비슷하도록) 케이크를 나누면 된다.
예를 들어, 1~18 / 19~25 로 나누면 완전탐색 했을 때 전자는 약 424만, 후자는 약 142만 정도의 경우의 수가 나온다.
충분히 MITM을 돌려볼 만한 경우의 수임을 알 수 있다.
DP를 적절히 섞어 중복을 제거하면 경우의 수를 약 1/10로 줄일 수 있지만, 여기까지 하지 않아도 AC가 나올 수 있도록 시간제한을 조정했다.

H. 크림 파스타
https://www.acmicpc.net/problem/25214
25214번: 크림 파스타
각 Ai가 추가된 직후의 문제의 답 N개를 공백으로 구분하여 출력한다.
www.acmicpc.net
배열의 맨 뒤에 수를 추가했을 때 답은 둘 중 하나이다.
1. 이전의 답
2. 맨 뒤에 추가한 수 - 현재 배열에서 가장 작은 수
따라서 이전의 답과 배열의 최소값을 유지해가며 O(N)에 문제를 풀 수 있다.
I. 타이핑
https://www.acmicpc.net/problem/25215
25215번: 타이핑
민겸이는 영어 소문자와 대문자로 이루어진 문자열을 타이핑하기로 했다. 민겸이가 사용할 수 있는 버튼은 26개의 영어 알파벳 버튼과 마름모(◆) 버튼, 별(★) 버튼이다. 각 버튼은 아래와 같이
www.acmicpc.net
점화식이 쉽게 나오기 때문에 DP로도 풀 수 있고, 잘 생각해보면 그리디로도 풀 수 있다.
위의 H번 문제와 더불어 적절한 실버 난이도의 문제들이었다고 생각한다.
J. 파밍 루트
https://www.acmicpc.net/problem/25216
25216번: 파밍 루트
경태는 인하대학교에서 유행하는 게임 Conquer The Planet(이하 CTP)에 빠져있다. CTP를 열심히 플레이하던 어느 날, 경태는 게임 속에 숨겨져 있던 던전을 발견했다! 던전 입구에는 플레이어를 위한 설
www.acmicpc.net
원래는 이렇게까지 복잡한 문제는 아니었는데, 내 요청으로 이것저것 추가하다보니 문제가 살짝 지저분해졌다.
아픈게 싫으니까 방어력에 올인한 사람이 있다면, 강한 것이 좋으니까 공격력에 올인한 사람도 있어야 한다.
플레이어의 방어력을 고정해보자. 얻을 수 있는 최대 금화가 얼마인지 DP로 구할 수 있음을 알 수 있다.
방어력이 늘어나면 얻을 수 있는 금화도 늘어나고, 줄어들면 얻을 수 있는 금화도 줄어드므로 파라메트릭 서치를 이용할 수 있음을 알 수 있다. 얻을 수 있는 최대 금화를 계산한 다음, 이 금화를 얻을 수 있는 방어력의 최솟값을 이분탐색으로 찾으면 된다.
이분탐색 없이 DP 한 번으로도 풀 수 있다. DP 테이블에 {금화, 방어력} 쌍을 저장하면 된다.
결과

교내대회는 총 8문제가 풀렸고, 1등은 7솔을 했다.
J를 36트라이해서 유일하게 AC를 받은 상남자가 눈에 띈다.
개인적으로 C와 J는 그렇다 치고 E(샤카샤카)는 누군가 풀어주길 바랬었는데, 그러지 못해 아쉬웠다.
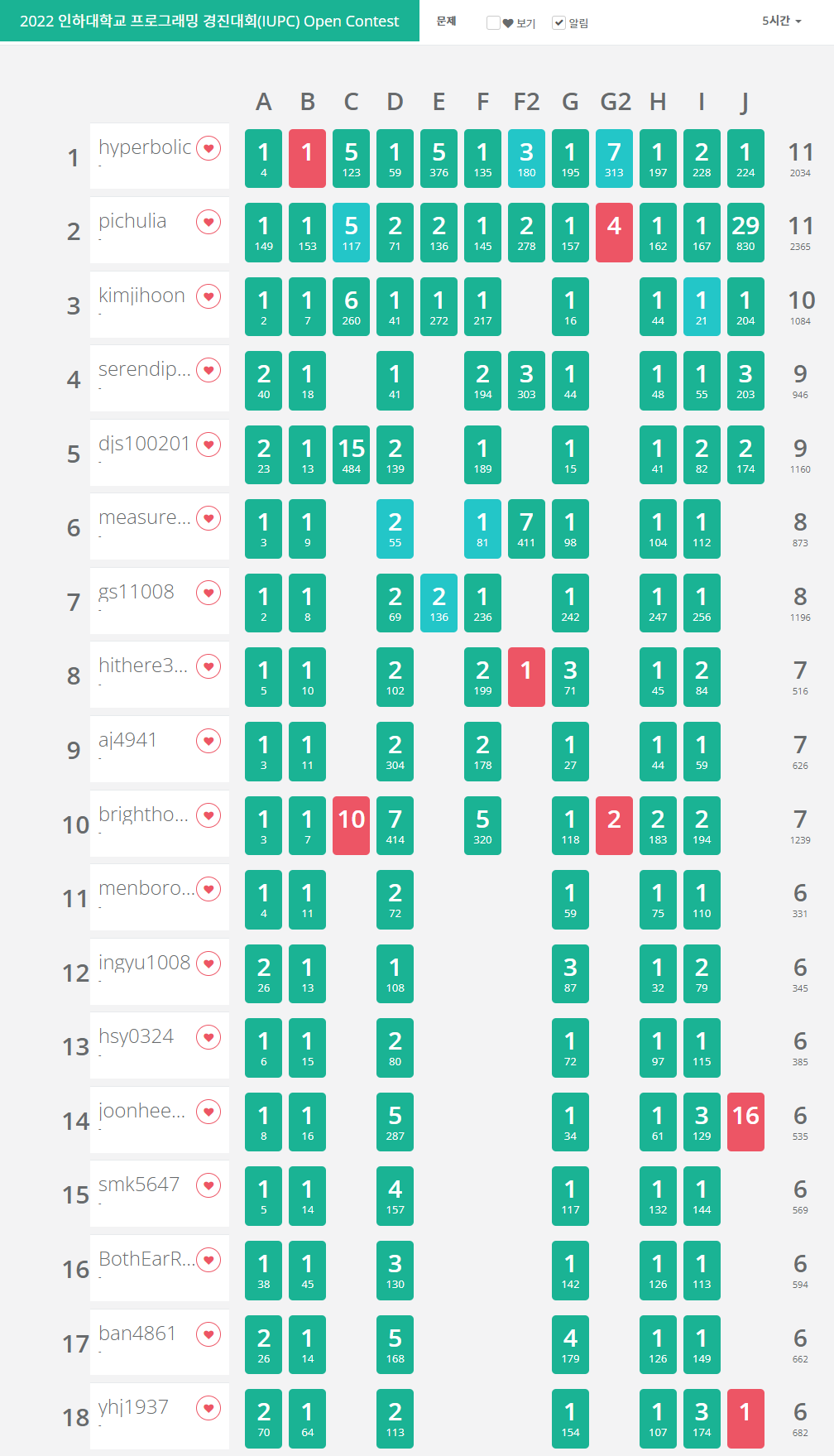
매우 아쉽게도 이번에는 올솔이 나오지 않았다. 이번에는 인하대학교 출제진의 승리이다(?)
하지만 스코어보드를 보니 확실히 Hard 두 문제를 추가한게 옳은 선택이었다고 생각한다.
마지막으로, 출제진과 검수진이 매긴 문제들의 난이도는 다음과 같았다. (평균)
이번엔 신박한 문제들이 꽤 있어서 난이도를 가늠하기 어려웠던것 같다.
A. 경로당펑크 2077 - B2
B. 너의 평점은 - B2
C. 바벨탑의 저주 - P3
D. 새벽의 탐정 게임 - G4
E. 샤카샤카 - G2
F. 정사각형 세기 - G4
F2. 정사각형 세기 (Hard) - P3
G. 조각 케이크 - S1
G2. 조각 케이크 (Hard) - P1
H. 크림 파스타 - S2
I. 타이핑 - G5
J. 파밍 루트 - G1
마지막으로


재미있었다!
'잡담' 카테고리의 다른 글
| 2023 KAKAO BLIND RECRUITMENT 1차 코딩테스트 풀이 (10) | 2022.09.24 |
|---|---|
| 생존신고 (3) | 2022.09.02 |
| Code Jam Round 2 2022 (2) | 2022.05.15 |
| 근황 (0) | 2022.03.19 |
| 근황 (김) (3) | 2021.12.05 |



