최소 공통 조상(Least Common Ancestor, LCA)는 트리에 있는 정점 \(u, v\)에 대해, \(u\)와 \(v\)의 공통 조상 중 가장 가까운 것을 말합니다.
예를 들어 아래와 같은 트리에서,
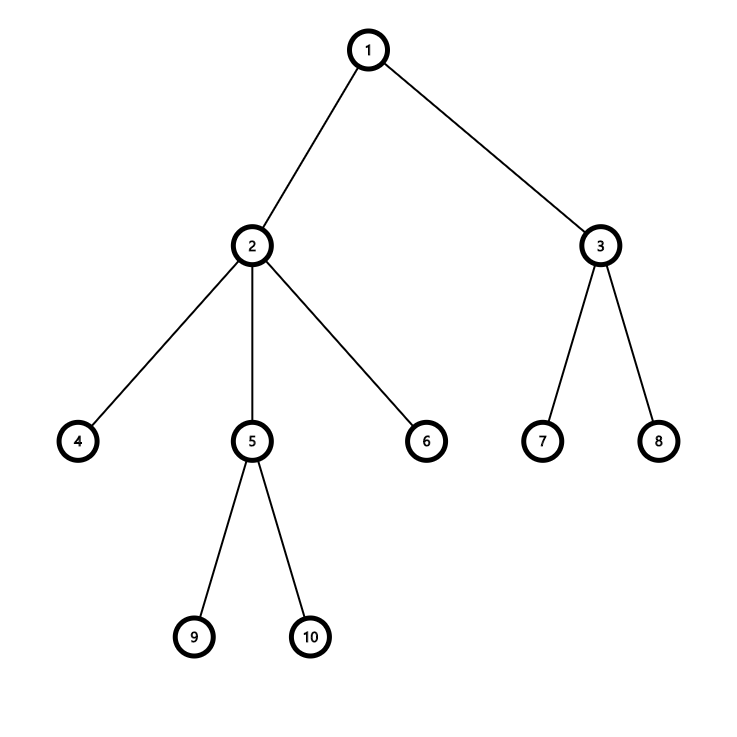
2번 정점과 7번 정점의 LCA는 1번 정점,
9번 정점과 4번 정점의 LCA는 2번 정점입니다.
그러면 LCA를 구하는 알고리즘에 대해 알아봅시다.
1. \(O(n)\) Navie
https://www.acmicpc.net/problem/11437
11437번: LCA
첫째 줄에 노드의 개수 N이 주어지고, 다음 N-1개 줄에는 트리 상에서 연결된 두 정점이 주어진다. 그 다음 줄에는 가장 가까운 공통 조상을 알고싶은 쌍의 개수 M이 주어지고, 다음 M개 줄에는 정점 쌍이 주어진다.
www.acmicpc.net
트리를 DFS등으로 탐색하면서 각 정점의 깊이와 부모를 저장합시다.
LCA를 알고 싶은 두 정점 \(u, v\)가 있으면, 두 정점의 깊이가 같아질 때까지 더 깊은 정점을 부모로 이동시켜줍시다.
그 후에 두 정점이 같아질 때까지 두 정점을 동시에 부모로 이동시켜주면 됩니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
|
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
ll gcd(ll a, ll b) { for (; b; a %= b, swap(a, b)); return a; }
int n, m;
vector <int> graph[50001];
int lv[50001];
int par[50001];
void DFS(int v, int p, int l)
{
lv[v] = l;
par[v] = p;
for (int nv : graph[v])
{
if (nv == p) continue;
DFS(nv, v, l + 1);
}
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n;
for (int i = 0; i < n - 1; i++)
{
int u, v; cin >> u >> v;
graph[u].push_back(v);
graph[v].push_back(u);
}
DFS(1, 0, 0);
cin >> m;
while (m--)
{
int u, v; cin >> u >> v;
int lv_u = lv[u], lv_v = lv[v];
while (lv_u > lv_v)
{
u = par[u];
lv_u--;
}
while (lv_v > lv_u)
{
v = par[v];
lv_v--;
}
while (u != v)
{
u = par[u];
v = par[v];
}
cout << u << '\n';
}
}
|
최악의 경우 모든 정점을 한번씩 방문하게 되므로, 시간복잡도는 \(O(n)\)입니다. (\(n : \) 트리의 정점의 개수)
스파스 테이블 (Sparse Table)
https://www.acmicpc.net/problem/17435
17435번: 합성함수와 쿼리
함수 f : {1, 2, ..., m}→{1, 2, ..., m}이 있다. 이때 fn : {1, 2, ..., m}→{1, 2, ..., m}을 다음과 같이 정의하자. f1(x) = f(x) fn+1(x) = f(fn(x)) 예를 들어 f4(1) = f(f(f(f(1))))이다. n과 x가 주어질 때 fn(x)를 계산하는 쿼리를 수행하는 프로그램을 작성하시오.
www.acmicpc.net
어떤 함수 \(f(x)\)에 대해, \(f_n(f_m(x)) = f_{n+m}(x)\)가 성립한다면 스파스 테이블을 이용해 \(f_n(x)\)를 \(O(\log n)\)에 구할 수 있습니다.
\(f_n(x)\)가 이미 계산되어 있다고 했을 때, \(f_{2n}(x)\)는 다음과 같은 식으로 쉽게 구할 수 있습니다.
$$f_{2n}(x) = f_n(f_n(x))$$
그러면 \(f(x), f_2(x), f_4(x), f_8(x), \dots\)를 미리 전처리로 구해 놓을 수 있게 되는데, 이를 이용해 \(a^n\)를 \(\log n\)에 구하는 방식과 똑같은 방법으로 \(f_n(x)\)를 구할 수 있게 됩니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
ll gcd(ll a, ll b) { for (; b; a %= b, swap(a, b)); return a; }
int m;
int sp[21][200001];
// sp[i][j] = f_{2^i}(j)
int main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> m;
for (int i = 1; i <= m; i++)
cin >> sp[0][i];
for (int i = 1; i <= 20; i++)
{
for (int j = 1; j <= m; j++)
sp[i][j] = sp[i - 1][sp[i - 1][j]];
}
int q; cin >> q;
while (q--)
{
int n, x; cin >> n >> x;
for (int i = 0; i <= 20; i++)
{
if (n & (1 << i)) x = sp[i][x];
}
cout << x << '\n';
}
}
|
시간복잡도는 전처리에 \(O(x\log n)\)이고,
\(f_n(x)\)를 구하는 쿼리당 \(O(\log n)\)입니다.
https://www.acmicpc.net/problem/11438
11438번: LCA 2
첫째 줄에 노드의 개수 N이 주어지고, 다음 N-1개 줄에는 트리 상에서 연결된 두 정점이 주어진다. 그 다음 줄에는 가장 가까운 공통 조상을 알고싶은 쌍의 개수 M이 주어지고, 다음 M개 줄에는 정�
www.acmicpc.net
위 스파스 테이블을 이용해 LCA를 효율적으로 구해봅시다.
\(f(x)\) 를 정점 \(x\)의 부모를 구하는 함수로 정의하면, \(f_n(f_m(x)) = f_{n+m}(x)\)가 성립하기 때문에 스파스 테이블을 사용할 수 있게 됩니다.
그러면 위에서 나이브로 풀 때의
'두 정점의 깊이가 같아질 때까지 더 깊은 정점을 부모로 이동시켜주는' 작업과,
'두 정점이 같아질 때까지 두 정점을 동시에 부모로 이동시켜주는' 작업을 스파스 테이블을 이용해 \(O(\log n)\)에 할 수 있게 됩니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
|
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
ll gcd(ll a, ll b) { for (; b; a %= b, swap(a, b)); return a; }
int n;
vector <int> graph[100001];
int lv[100001];
int sp[21][100001];
// sp[i][j] = f_{2^i}(j)
void DFS(int v, int p, int l)
{
sp[0][v] = p;
lv[v] = l;
for (int nv : graph[v])
{
if (nv == p) continue;
DFS(nv, v, l + 1);
}
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n;
for (int i = 0; i < n - 1; i++)
{
int u, v; cin >> u >> v;
graph[u].push_back(v);
graph[v].push_back(u);
}
DFS(1, 0, 0);
for (int i = 1; i <= 20; i++)
{
for (int j = 1; j <= n; j++)
sp[i][j] = sp[i - 1][sp[i - 1][j]];
}
int m; cin >> m;
while (m--)
{
int u, v; cin >> u >> v;
if (lv[u] > lv[v]) swap(u, v);
int d = lv[v] - lv[u];
for (int i = 0; i <= 20; i++)
{
if (d & (1 << i)) v = sp[i][v];
}
if (u == v)
{
cout << u << '\n';
continue;
}
for (int i = 20; i >= 0; i--)
{
if (sp[i][u] != sp[i][v])
{
u = sp[i][u];
v = sp[i][v];
}
}
cout << sp[0][u] << '\n';
}
}
|
시간복잡도는 역시 전처리에 \(O(n\log n)\),
LCA를 구하는 쿼리당 \(O(\log n)\)입니다.
제 그룹의 문제집에서 연습 문제들을 관리하고 있습니다.
문제집의 문제들을 보고 싶으시다면, 가입 신청을 해 주세요.
ANZ1217
무슨 내용을 넣어야 좋을까요?
www.acmicpc.net
'알고리즘 > 그래프' 카테고리의 다른 글
| Strongly Connected Component (0) | 2020.06.18 |
|---|---|
| Euler tour technique (0) | 2020.06.15 |
| 위상 정렬 (0) | 2020.05.10 |
| 최소 스패닝 트리 (0) | 2020.05.05 |
| 최단 경로 (0) | 2020.04.29 |



