그래프에서 두 정점 사이의 최단 경로를 구하는 알고리즘에 대해 알아봅시다.
BFS
간선의 가중치가 모두 1이라면(같다면), BFS를 이용해 한 정점에서 다른 정점들 사이의 최단 거리를 알 수 있습니다.
자세한 설명은
https://anz1217.tistory.com/21
그래프 탐색 (DFS, BFS)
그래프는 정점과 정점들을 잇는 간선들의 집합으로 이루어진 자료구조입니다. 이 글에서는 그래프를 저장하는 방법과, 그래프를 탐색하는 방법에 대해 알아보도록 합시다. 다음과 같은 그래프를 저장한다고 생각해..
anz1217.tistory.com
에서 볼 수 있습니다.
시간 복잡도는 \(O(|V|+|E|)\)입니다.
0-1 BFS
문제를 조금 확장해 봅시다.
간선의 가중치가 모두 0또는 1이라면 어떻게 최단 거리를 알 수 있을까요?
https://www.acmicpc.net/problem/13549
13549번: 숨바꼭질 3
수빈이는 동생과 숨바꼭질을 하고 있다. 수빈이는 현재 점 N(0 ≤ N ≤ 100,000)에 있고, 동생은 점 K(0 ≤ K ≤ 100,000)에 있다. 수빈이는 걷거나 순간이동을 할 수 있다. 만약, 수빈이의 위치가 X일 때 걷는다면 1초 후에 X-1 또는 X+1로 이동하게 된다. 순간이동을 하는 경우에는 0초 후에 2*X의 위치로 이동하게 된다. 수빈이와 동생의 위치가 주어졌을 때, 수빈이가 동생을 찾을 수 있는 가장 빠른 시간이 몇 초 후인지 구하는
www.acmicpc.net
BFS를 설명할 때 풀어본 문제인데, 문제 상황이 조금 바뀌었습니다.
위치 \(x\)에서 \(x \times 2\)로 갈 때는 1초가 아니라, 0초 걸린다고 합니다.
BFS탐색은 그래프를 '정점에서 떨어진 거리'에 따라 순차적으로 방문하는 탐색방법입니다.
현재 큐의 맨 앞에 있는 정점을 탐색하고 있다고 하고, 정점에 연결되어 있으면서 아직 방문하지 않은 정점을 큐의 맨 뒤에 삽입하면 정점이 '거리 순으로' 큐 안에 저장되게 됩니다.

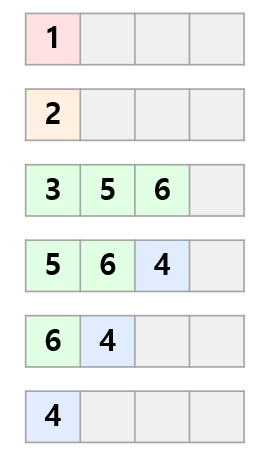
그런데 간선의 가중치가 0인 경우가 있으면 조금 상황이 다릅니다.
현재 정점 \(u\)를 탐색하고 있고, 아직 탐색하지 않았으면서 \(u\)와 가중치 0인 간선으로 연결된 정점 \(v\)가 있다고 합시다.
하지만 \(v\)를 하던대로 큐의 맨 끝에 삽입하게 되면 큐 안에서는 거리 순으로 저장되지 않을 수 있습니다.
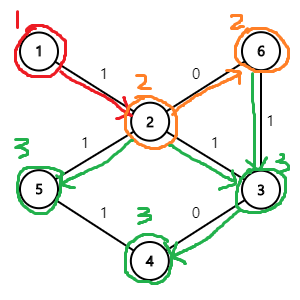
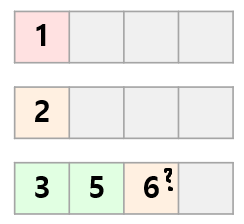
이러면 최단거리가 제대로 계산되지 않게 되기 때문에, 다른 방법을 생각해야 합니다.
가중치가 0이라면 큐의 맨 끝이 아니라, 맨 앞에 삽입하면 단계별로 나눌 수 있지 않을까요?
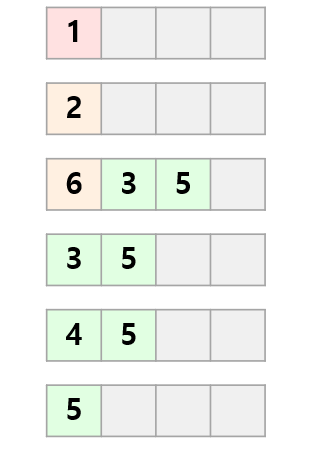
그렇습니다. 가중치가 0인 경우는 큐의 맨 앞에, 1인 경우는 큐의 맨 뒤에 삽입하는 식으로 BFS를 진행하면,
무조건 가중치가 0인 (같은 거리인) 정점을 먼저 탐색할 수 있게 되므로, 큐 내부에서 단계별로 나눠질 수 있게 됩니다.
자료구조만 바뀌고 BFS와 완전히 같기 때문에 시간복잡도는 역시 \(O(|V|+|E|)\)입니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
|
#include <iostream>
#include <algorithm>
#include <cstring>
#include <deque>
using namespace std;
int n, k;
int dist[100001];
int main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> k;
memset(dist, -1, sizeof dist);
deque <int> dq; // 큐의 앞에 삽입하는 작업을 위해 deque를 사용한다.
dq.push_back(n);
dist[n] = 0;
while (!dq.empty())
{
int v = dq.front(); dq.pop_front();
if (v * 2 <= 100000 && dist[v * 2] == -1)
{
// 두 점 사이의 거리가 0이면 큐의 앞에 추가한다.
dq.push_front(v * 2);
dist[v * 2] = dist[v];
}
if (v - 1 >= 0 && dist[v - 1] == -1)
{
dq.push_back(v - 1);
dist[v - 1] = dist[v] + 1;
}
if (v + 1 <= 100000 && dist[v + 1] == -1)
{
dq.push_back(v + 1);
dist[v + 1] = dist[v] + 1;
}
}
cout << dist[k];
}
|
다익스트라 알고리즘 (Dijkstra Algorithm)
문제를 더 일반적으로 확장해봅시다.
그래프의 가중치가 0, 1 뿐만 아니라 어떤 0 이상의 수라도 될 수 있다면, 어떻게 최단 경로를 구할 수 있을까요?
앞에서 큐 안에 정점이 저장될 때, 시작 정점에서 떨어진 거리 순으로 저장되어야 한다고 했습니다.
0-1 BFS에서는 가중치가 0일 때는 큐의 앞에, 1일 때는 큐의 뒤에 저장하는 방식으로 이를 해결 했습니다.
하지만 가중치가 어떤 수든 될 수 있기 때문에, 거리 순으로 큐에 저장하려면 큐의 앞뒤 뿐만아니라 중간에 저장해야하는 경우가 생기게 됩니다.
일반적인 선형 자료구조(배열, 큐, 덱)등으로는 이 작업을 빠르게 할 수 없습니다.
그렇다면 원소들을 크기 순으로 정렬한 채로 유지하면서, 원소의 추가와 삭제에 시간이 얼마 걸리지 않는 자료구조가 필요합니다.
가장 쉽게 생각할 수 있는 건 균형 이진 탐색 트리(set)입니다.
set을 사용하면 안의 원소들이 시작정점에서 떨어진 순으로 유지하면서, 삽입과 삭제에 \(\log N\)의 시간만이 걸리기 때문에 이를 해결하기 위해 적합한 자료구조입니다.
다음 문제를 풀어봅시다.
https://www.acmicpc.net/problem/1753
1753번: 최단경로
첫째 줄에 정점의 개수 V와 간선의 개수 E가 주어진다. (1≤V≤20,000, 1≤E≤300,000) 모든 정점에는 1부터 V까지 번호가 매겨져 있다고 가정한다. 둘째 줄에는 시작 정점의 번호 K(1≤K≤V)가 주어진다. 셋째 줄부터 E개의 줄에 걸쳐 각 간선을 나타내는 세 개의 정수 (u, v, w)가 순서대로 주어진다. 이는 u에서 v로 가는 가중치 w인 간선이 존재한다는 뜻이다. u와 v는 서로 다르며 w는 10 이하의 자연수이다. 서로 다른 두
www.acmicpc.net
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
|
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <set>
using namespace std;
const int INF = 1e9;
int v, e;
int k;
vector <pair<int, int> > graph[20001];
// 각 정점에 대해 {연결된 정점, 가중치} pair을 저장하고 있는 인접 리스트
int dist[20001];
int main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
fill(dist, dist + 20001, INF); // INF 값으로 초기화한다.
cin >> v >> e >> k;
for (int i = 0; i < e; i++)
{
int u, v, w;
cin >> u >> v >> w;
graph[u].push_back({ v,w });
}
set <pair<int, int> > st;
// {시작 정점에서의 거리, 정점 번호}를 거리가 작은 순으로 저장한다.
st.insert({ 0, k });
dist[k] = 0;
while (!st.empty())
{
int v = st.begin()->second;
st.erase(st.begin());
for (auto it : graph[v])
{
int nv = it.first;
int w = it.second;
if (dist[nv] > dist[v] + w)
{
// 현재 저장된 (시작 -> nv까지의 거리)보다
// (시작 -> v -> nv의 거리)가 더 짧다면
st.erase({ dist[nv], nv });
dist[nv] = dist[v] + w;
st.insert({ dist[nv], nv });
// set에 저장되어 있는 값을 갱신해준다.
}
}
}
for (int i = 1; i <= v; i++)
{
if (dist[i] == INF) cout << "INF\n";
else cout << dist[i] << '\n';
}
}
|
그런데 잘 생각해보면, 자료구조 내에서 원소가 꼭 "정렬되어 있는 상태"로 있을 필요는 없다는 것을 알 수 있습니다.
실제로 자료구조 내에서 원소가 어떻게 저장되어 있든지 상관없이,
아무튼 삽입과 삭제가 빠르게 가능하고 가장 작은 원소를 가져올 수 있으면 되는데, 따라서 힙 (우선순위 큐)를 이용해서도 똑같이 풀 수 있습니다.
대신 힙은 임의 원소의 삭제가 불가능하기 때문에, 실제 dist 배열에 저장된 정점까지의 거리와 힙에 저장된 거리가 서로 다르다면 무시하는 방법으로 처리하면 됩니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
|
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <queue>
using namespace std;
const int INF = 1e9;
int v, e;
int k;
vector <pair<int, int> > graph[20001];
// 각 정점에 대해 {연결된 정점, 가중치} pair을 저장하고 있는 인접 리스트
int dist[20001];
int main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
fill(dist, dist + 20001, INF); // INF 값으로 초기화한다.
cin >> v >> e >> k;
for (int i = 0; i < e; i++)
{
int u, v, w;
cin >> u >> v >> w;
graph[u].push_back({ v,w });
}
priority_queue<pair<int, int> > pq;
// {시작 정점에서의 거리, 정점 번호}를 거리가 작은 순으로 저장한다.
pq.push({ 0, k });
dist[k] = 0;
while (!pq.empty())
{
int v = pq.top().second;
int d = -pq.top().first;
pq.pop();
if (dist[v] != d) continue;
// 힙에 저장되어있는 거리와 dist배열에 저장된 거리가 다르다면
// 이전에 삭제된 값이기 때문에 무시한다.
for (auto it : graph[v])
{
int nv = it.first;
int w = it.second;
if (dist[nv] > dist[v] + w)
{
// 현재 저장된 (시작 -> nv까지의 거리)보다
// (시작 -> v -> nv의 거리)가 더 짧다면
dist[nv] = dist[v] + w;
pq.push({ -dist[nv], nv });
// 갱신해서 pq에 삽입한다.
// pq는 기본적으로 수가 큰 순으로 pop하기 때문에 부호를 바꿔 넣어준다.
}
}
}
for (int i = 1; i <= v; i++)
{
if (dist[i] == INF) cout << "INF\n";
else cout << dist[i] << '\n';
}
}
|
시간복잡도를 계산해 봅시다.
모든 정점과 간선을 한번씩 살펴보는 것은 BFS랑 같지만, 지금까지와는 달리 값의 삽입, 삭제에 \(O(\log N)\)이 걸리는 자료구조를 사용하고 있습니다.
그러므로 일단 \(O((|V|+|E|)\log N)\)의 시간복잡도를 가지게 됩니다.
(\(N :\) 자료구조에 저장될 수 있는 최대 원소의 개수)
각각의 자료구조에 원소가 최대 몇 개 들어갈 수 있는지 살펴봅시다.
set을 사용한 경우 중간 삭제가 가능하기 때문에 많아도 \(|V|\)개의 원소가 저장되어 있게 됩니다.
따라서 이 경우 시간복잡도는 \(O((|V|+|E|)\log |V|)\) 입니다.
priority_queue를 사용한 경우는 중간 삭제가 불가능합니다.
따라서 원소가 중복해서 들어갈 수 있게 되는데, 최악의 경우 \(|E|\)개의 원소가 저장되게 됩니다.
따라서 시간복잡도는 \(O((|V|+|E|)\log |E|)\) 인데, 일반적으로 \(|E| \le |V|^2\)이기 때문에
\(O((|V|+|E|)\log |E|)\)
\(= O((|V|+|E|)\log |V|^2)\)
\(=O((|V|+|E|)\log |V|) \) 입니다.
따라서 두 방법 모두 시간복잡도는 같지만,
삽입/삭제 연산을 할 때 set의 경우 상수가 커서 같은 \(\log N\)이라도 더 많은 시간이 걸리기 때문에, priority_queue를 쓰는 것이 조금 더 빠릅니다.
벨만-포드 알고리즘 (Bellman-Ford Algorithm)
위의 다익스트라 알고리즘은 대부분의 최단 경로를 구하는 문제에 쓸 수 있지만, 이 알고리즘을 쓰지 못하는 특수한 경우가 있습니다.
바로 간선의 가중치가 음수인 경우입니다.

위의 그래프에서 1번 정점에서 5번 정점까지의 거리를 다익스트라 알고리즘을 이용해 계산한다고 생각해 봅시다.
먼저 1, 2, 4, 5번 정점이 차례대로 탐색되는 것은 자명합니다.
1번에서 3번 정점으로의 가중치가 6이기 때문에, 3번 정점은 그 이후에 탐색되게 됩니다.
그런데 그 이후의 상황을 봅시다. 3번에서 4번 정점으로의 가중치가 음수이고, 4번 정점까지의 최단 거리가 갱신되었습니다.
따라서 이미 4번 정점을 한 번 방문했음에도 불구하고, 다시 4번 정점에서 시작하여 최단거리를 갱신해 나가게 됩니다.
이와 같이 간선의 가중치가 음수인 경우가 있을 때 다익스트라 알고리즘을 사용하면, 같은 정점을 여러 번 방문하게 되므로 최악의 경우 지수 시간이 걸리게 됩니다.
또 다음과 같이 음수 사이클이 존재한다면 알고리즘이 끝나지 않고 무한히 동작하게 됩니다.
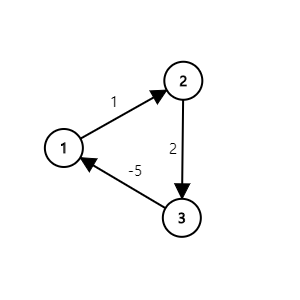
따라서 음수 가중치를 가지는 간선이 있는 경우에도 빠르게 최단 경로를 찾거나, 음수 사이클이 있음을 감지할 수 있는 다른 알고리즘이 필요하게 됩니다.
https://www.acmicpc.net/problem/11657
11657번: 타임머신
첫째 줄에 도시의 개수 N (1 ≤ N ≤ 500), 버스 노선의 개수 M (1 ≤ M ≤ 6,000)이 주어진다. 둘째 줄부터 M개의 줄에는 버스 노선의 정보 A, B, C (1 ≤ A, B ≤ N, -10,000 ≤ C ≤ 10,000)가 주어진다.
www.acmicpc.net
다익스트라 알고리즘에서 어떤 간선 \((u,v)\)가 있을 때, (시작점에서 \(v\)까지의 거리)보다 (시작점에서 \(u\)까지의 거리) + (\((u,v)\)의 가중치)가 더 작으면 값을 갱신해 주는 부분이 있었습니다.
"모든 간선을 이용해 정점까지의 거리를 갱신한다"는 작업을 반복하는 것만으로 최단거리를 구해보면 어떨까요?
시작 정점까지의 거리를 0으로, 나머지를 \(\infty\)로 두고 시작합시다.

먼저 \((1,2)\)간선을 이용해 2번 정점까지의 거리가 2로 갱신됩니다.
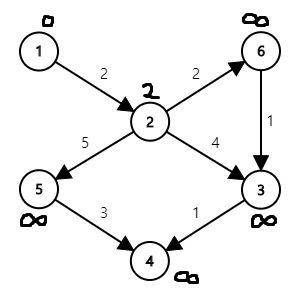
다음은 \((2,3)\), \((2,5)\), \((2,6)\) 간선을 각각 이용해
3번 정점까지의 거리가 6,
5번 정점까지의 거리가 7,
6번 정점까지의 거리가 4로 갱신됩니다.
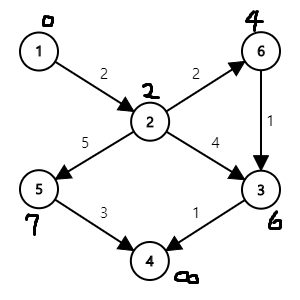
다음은 \((4,3)\), \((5,4)\) 간선을 각각 이용해
3번 정점까지의 거리가 5,
4번 정점까지의 거리가 10으로 갱신됩니다.
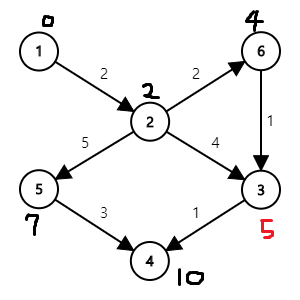
마지막으로 간선 \((3,4)\)를 이용해 4번 정점까지의 거리가 6으로 갱신됩니다.

이런 방식으로 최단거리를 구할 수 있다는 건 알겠는데, 모든 간선을 이용해 정점까지의 거리를 갱신하는 이 작업을 최대 몇 번 반복해야 할까요?
정점이 \(|V|\)개 일 때, 어떤 정점 \(u\)에서 \(v\)까지의 최단 경로에 포함되는 간선의 개수는 최대 \(|V|-1\)개입니다.
따라서 위의 작업을 총 \(|V|-1\)번 반복하면 시작 정점에서 다른 모든 정점까지의 최단 경로를 구할 수 있음을 알 수 있습니다.
음수 사이클이 존재할 경우에는 어떻게 감지할 수 있을까요?
위 작업을 \(|V|-1\)회 반복한 후에 한번 더 모든 간선을 이용해 최단거리를 갱신해봅시다.
만약 그래도 최단 거리가 갱신되는 경우가 생긴다면, 어딘가에 음수 사이클이 있어서 무한히 최단거리가 갱신되는 경우일 것입니다.
음수 사이클이 존재할 때, dist배열에 저장된 거리가 int범위를 벗어날 수 있음에 주의합시다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
|
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <queue>
using namespace std;
const long long INF = 1e9;
int n, m;
vector <pair<int, int> > graph[501];
// 각 정점에 대해 {연결된 정점, 가중치} pair을 저장하고 있는 인접 리스트
long long dist[501];
int main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
fill(dist, dist + 501, INF); // INF 값으로 초기화한다.
cin >> n >> m;
for (int i = 0; i < m; i++)
{
int u, v, w; cin >> u >> v >> w;
graph[u].push_back({ v,w });
}
dist[1] = 0; // 시작점까지의 거리는 0이다.
for (int k = 0; k < n - 1; k++) // v-1회 반복
{
for (int v = 1; v <= n; v++)
{
for (auto it : graph[v]) // 모든 간선에 대해 살펴본다.
{
int nv = it.first;
int w = it.second;
if (dist[v] != INF && dist[nv] > dist[v] + w)
{
dist[nv] = dist[v] + w;
// 이 간선을 이용해 최단 거리를 갱신할 수 있으면 갱신한다.
}
}
}
}
for (int v = 1; v <= n; v++)
{
for (auto it : graph[v]) // 모든 간선에 대해 살펴본다.
{
int nv = it.first;
int w = it.second;
if (dist[v] != INF && dist[nv] > dist[v] + w)
{
// 만약 그래도 아직 갱신할 수 있다면 음수 사이클이 존재한다.
cout << -1;
return 0;
}
}
}
for (int i = 2; i <= n; i++)
{
if (dist[i] == INF) cout << "-1\n";
else cout << dist[i] << '\n';
}
}
|
시간복잡도는 모든 간선에 대해 살펴보는 작업을 \(|V|-1\)회 반복하므로 \(O(|V||E|)\)입니다.
이 벨만-포드 알고리즘을 좀 더 최적화 한 SPFA(Shortest Path Faster Algorithm)라는 알고리즘이 있습니다.
벨만-포드는 정점이 갱신이 되는지 여부와 상관없이, 아무튼 모든 간선을 이용해서 최단 거리를 갱신하는 작업을 반복하는데,
SPFA는 거리가 실제로 갱신된 정점에 연결된 간선만을 이용해서 최단 거리를 갱신합니다.
또 음수 사이클 감지는 어떤 정점이 \(|V|\)회 이상 방문되는지 여부를 확임함으로써 감지할 수 있습니다.
음수 사이클이 없다면 모든 정점은 많아도 \(|V|-1\)회 방문되기 때문입니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
|
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <queue>
using namespace std;
const long long INF = 1e9;
int n, m;
vector <pair<int, int> > graph[501];
// 각 정점에 대해 {연결된 정점, 가중치} pair을 저장하고 있는 인접 리스트
long long dist[501];
int visited_cnt[501]; // 방문 횟수 저장
bool inQueue[501]; // 현재 이 정점이 큐 안에 있는지 저장
int main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
fill(dist, dist + 501, INF); // INF 값으로 초기화한다.
cin >> n >> m;
for (int i = 0; i < m; i++)
{
int u, v, w; cin >> u >> v >> w;
graph[u].push_back({ v,w });
}
dist[1] = 0; // 시작점까지의 거리는 0이다.
queue <int> q; // 다음 갱신할 정점을 큐로 관리한다.
q.push(1);
inQueue[1] = 1;
while (!q.empty())
{
int v = q.front(); q.pop();
inQueue[v] = 0;
if (++visited_cnt[v] >= n)
{
// 어떤 정점이 v회 이상 방문되었다면 음수 사이클이 존재한다.
cout << -1;
return 0;
}
for (auto it : graph[v])
{
int nv = it.first;
int w = it.second;
if (dist[nv] > dist[v] + w)
{
dist[nv] = dist[v] + w;
// 정점이 갱신된 경우에만 큐에 넣는다.
// 만약 이미 큐 안에 있다면 또 넣지 않는다.
if (!inQueue[nv])
{
inQueue[nv] = 1;
q.push(nv);
}
}
}
}
for (int i = 2; i <= n; i++)
{
if (dist[i] == INF) cout << "-1\n";
else cout << dist[i] << '\n';
}
}
|
SPFA도 최악의 경우 \(O(|V||E|)\)의 시간복잡도를 가지지만, 평균적으로는 \(O(|E|)\)의 속도로 다익스트라 보다도 빠르게 최단경로를 구할 수 있게 됩니다.
플로이드-워셜 알고리즘 (Floyd-Warshall Algortihm)
마지막으로 모든 정점에서 모든 정점까지의 최단경로를 구하는 플로이드-워셜 알고리즘에 대해 알아봅시다.
플로이드-워셜은 모든 정점 쌍 \((u,v)\)에 대해, 어떤 정점 \(a\)를 중간 정점으로 해서 최단 경로를 갱신할 수 있는지 살펴봅니다.
다시 말하면, \(u \rightarrow v\)까지의 거리보다 \(u \rightarrow a \rightarrow v\)가 더 짧으면 최단 경로를 후자로 갱신합니다.
이 작업을 모든 정점을 한번 씩 \(a\)로 설정해서 \(|V|\)회 반복하고 나면 모든 정점 사이에 최단 경로를 구할 수 있게 됩니다.
https://www.acmicpc.net/problem/11404
11404번: 플로이드
첫째 줄에 도시의 개수 n(1 ≤ n ≤ 100)이 주어지고 둘째 줄에는 버스의 개수 m(1 ≤ m ≤ 100,000)이 주어진다. 그리고 셋째 줄부터 m+2줄까지 다음과 같은 버스의 정보가 주어진다. 먼저 처음에는 그 버스의 출발 도시의 번호가 주어진다. 버스의 정보는 버스의 시작 도시 a, 도착 도시 b, 한 번 타는데 필요한 비용 c로 이루어져 있다. 시작 도시와 도착 도시가 같은 경우는 없다. 비용은 100,000보다 작거나 같은 자연수이다. 시작
www.acmicpc.net
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
|
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <queue>
using namespace std;
const int INF = 1e9;
int n, m;
int dist[101][101];
int main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m;
fill(&dist[0][0], &dist[100][100], INF);
for (int v = 1; v <= n; v++) dist[v][v] = 0;
// 같은 정점까지의 거리는 0이다.
for (int i = 0; i < m; i++)
{
int u, v, w; cin >> u >> v >> w;
dist[u][v] = min(dist[u][v], w);
}
for (int k = 1; k <= n; k++) // 모든 정점을 한번씩 중간 정점 k로 선택한다.
{
for (int i = 1; i <= n; i++) for (int j = 1; j <= n; j++)
{
//모든 정점 쌍 (i,j)에 대하여
// i->j 거리 보다 i->k->j가 더 짧다면 갱신한다.
if (dist[i][j] > dist[i][k] + dist[k][j])
dist[i][j] = dist[i][k] + dist[k][j];
}
}
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
{
if (dist[i][j] == INF) cout << "0 ";
else cout << dist[i][j] << ' ';
}
cout << '\n';
}
}
|
시간복잡도는 모든 정점 쌍을 \(|V|\)번 갱신하므로 \(O(|V|^3)\)입니다.
다익스트라나 벨만 포드를 \(|V|\)번 반복하는 것보다 훨씬 빠릅니다.
또 정점의 개수가 작은 그래프에 대해서 최단 경로를 구할 때, 복잡한 다익스트라나 벨만-포드 알고리즘을 쓰는 대신 코드가 짧고 간단한 플로이드-워셜 알고리즘을 쓰는게 더 효율적일 수도 있습니다.
음수 사이클도 감지할 수 있는데, 알고리즘을 실행한 후에 어떤 정점 \(v\)에서 \(v\)로 가는 거리가 음수인 경우가 있다면 음수 사이클이 존재함을 알 수 있습니다.
요약
가중치가 모두 같은 그래프, 단일 시작점 최단거리 : \(O(V+E)\) BFS
가중치가 모두 0이나 1인 그래프, 단일 시작점 최단거리 : \(O(V+E)\) 0-1 BFS
가중치가 0 이상인 그래프, 단일 시작점 최단거리 : \(O((V+E)\log V)\) 다익스트라
음수 가중치가 존재하는 그래프, 단일 시작점 최단거리 : \(O(VE)\) 벨만포드, SPFA (평균 \(O(E)\))
다중 시작점 최단거리 : \(O(V^3)\) 플로이드 워셜
제 그룹의 문제집에서 연습 문제들을 관리하고 있습니다.
문제집의 문제들을 보고 싶으시다면, 가입 신청을 해 주세요.
https://www.acmicpc.net/group/7712
ANZ1217
무슨 내용을 넣어야 좋을까요?
www.acmicpc.net
'알고리즘 > 그래프' 카테고리의 다른 글
| Euler tour technique (0) | 2020.06.15 |
|---|---|
| 최소 공통 조상 (0) | 2020.05.11 |
| 위상 정렬 (0) | 2020.05.10 |
| 최소 스패닝 트리 (0) | 2020.05.05 |
| 그래프 탐색 (DFS, BFS) (0) | 2020.04.28 |



