Strongly Connected Component (SCC)는 방향 그래프에서, 다음 조건을 만족하는 정점의 부분집합을 말합니다.
1. 부분집합에서 어떻게 두 정점 \(u,v\)를 선택하더라도 \(u\)에서 \(v\)로 가는 경로가 존재한다.
2. 부분집합에 속한 정점 \(u\)와 그렇지 않은 정점 \(v\)에 대해서, \(u\)에서 \(v\)로 가는 경로와 \(v\)에서 \(u\)로 가는 경로가 동시에 존재하지 않는다.
따라서 다음과 같은 방향 그래프는,
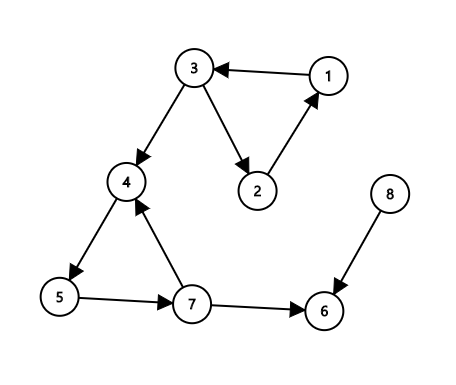
다음과 같이 4개의 SCC로 분할됩니다.
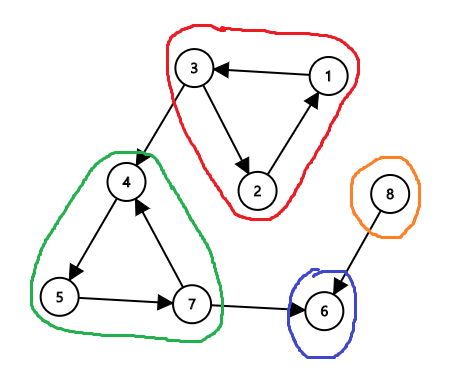
그래프를 이와같이 SCC로 분할하여 하나의 SCC를 하나의 정점으로 대체하면 그래프를 DAG로 나타낼 수 있게 됩니다.
일반적인 그래프를 DAG로 바꾸고 나면 위상정렬이나 DP등 다양한 작업을 할 수 있게 됩니다.
https://www.acmicpc.net/problem/2150
2150번: Strongly Connected Component
첫째 줄에 두 정수 V(1≤V≤10,000), E(1≤E≤100,000)가 주어진다. 이는 그래프가 V개의 정점과 E개의 간선으로 이루어져 있다는 의미이다. 다음 E개의 줄에는 간선에 대한 정보를 나타내는 두 정수 A, B
www.acmicpc.net
그러면 SCC를 구하는 알고리즘에 대해 알아봅시다.
1. 코사라주 알고리즘 (Kosaraju's Algorithm)
그래프를 DFS로 탐색한다음, 정점의 탐색이 끝난 순서대로 스택에 저장합니다.
그 다음 스택에 저장된 정점을 하나씩 pop하면서, 그래프의 간선이 반대로 된 그래프에 대해 pop한 정점에서 시작하는 DFS를 돌립니다.
이 때, 한 번의 DFS로 탐색되는 모든 정점은 하나의 SCC에 속합니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
|
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
ll gcd(ll a, ll b) { for (; b; a %= b, swap(a, b)); return a; }
int v, e;
vector <int> graph[10001];
vector <int> rgraph[10001];
vector<vector<int> > SCC;
int cache[10001];
vector <int> stk;
void DFS(int v)
{
cache[v] = 1;
for (int nv : graph[v])
{
if (!cache[nv]) DFS(nv);
}
stk.push_back(v);
}
void DFS2(int v)
{
cache[v] = 1;
SCC.back().push_back(v);
for (int nv : rgraph[v])
{
if (!cache[nv]) DFS2(nv);
}
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> v >> e;
for (int i = 0; i < e; i++)
{
int u, v; cin >> u >> v;
graph[u].push_back(v);
rgraph[v].push_back(u);
}
for (int i = 1; i <= v; i++)
{
if (!cache[i]) DFS(i);
}
memset(cache, 0, sizeof cache);
while (!stk.empty())
{
int i = stk.back(); stk.pop_back();
if (!cache[i])
{
SCC.emplace_back();
DFS2(i);
sort(SCC.back().begin(), SCC.back().end());
}
}
sort(SCC.begin(), SCC.end());
cout << SCC.size() << '\n';
for (auto& it : SCC)
{
for (int v : it) cout << v << ' ';
cout << "-1\n";
}
}
|
2. 타잔 알고리즘 (Tarjan's Algorithm)
그래프를 DFS로 탐색하면서, 정점을 탐색하는 순서대로 번호를 새로 붙입시다. 이를 \(DFS\_num[v]\)이라고 합시다.
또, 정점을 탐색하는 순서대로 스택에 저장합니다.
그리고 어떤 정점 \(v\)에서부터 시작해 이동하는 경로가 존재하면서, 현재 DFS로 탐색 중인 모든 정점 \(u\)에 대해, \(\min(DFS\_num[u])\)를 \(DFS\_min[v]\)라고 합시다.
DFS를 하던 도중, 정점 \(v\)에서 \(DFS\_num[v] = DFS\_min[v]\)라면, 스택 내에서 \(v\)보다 나중에 삽입된 정점은 모두 하나의 SCC에 속합니다.
마지막으로 이 정점들을 스택에서 제거하고, 탐색 완료했다고 표시합시다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
|
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
ll gcd(ll a, ll b) { for (; b; a %= b, swap(a, b)); return a; }
int v, e;
vector <int> graph[10001];
vector<vector<int> > SCC;
int DFS_cnt = 1;
int DFS_num[10001];
int DFS_min[10001];
int cache[10001];
vector <int> stk;
void DFS(int v)
{
cache[v] = 1;
DFS_num[v] = DFS_min[v] = DFS_cnt++;
stk.push_back(v);
for (int nv : graph[v])
{
if (!DFS_num[nv]) DFS(nv);
if (cache[nv]) DFS_min[v] = min(DFS_min[v], DFS_min[nv]);
}
if (DFS_num[v] == DFS_min[v])
{
SCC.emplace_back();
while (true)
{
int tv = stk.back();
SCC.back().push_back(tv);
cache[tv] = 0;
stk.pop_back();
if (tv == v) break;
}
sort(SCC.back().begin(), SCC.back().end());
}
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> v >> e;
for (int i = 0; i < e; i++)
{
int u, v; cin >> u >> v;
graph[u].push_back(v);
}
for (int i = 1; i <= v; i++)
{
if (!DFS_num[i]) DFS(i);
}
sort(SCC.begin(), SCC.end());
cout << SCC.size() << '\n';
for (auto& it : SCC)
{
for (int v : it) cout << v << ' ';
cout << "-1\n";
}
}
|
https://www.acmicpc.net/problem/11281
11281번: 2-SAT - 4
첫째 줄에 변수의 개수 N (1 ≤ N ≤ 10,000)과 절의 개수 M (1 ≤ M ≤ 100,000)이 주어진다. 둘째 줄부터 M개의 줄에는 절이 주어진다. 절은 두 정수 i와 j (1 ≤ |i|, |j| ≤ N)로 이루어져 있으며, i와 j가 ��
www.acmicpc.net
SCC를 이용해 풀 수 있는 대표적인 문제가 바로 2-SAT이라는 문제입니다.
2-SAT이 어떤 문제인지에 대한 설명은 링크를 참고합시다.
2-SAT 문제에서 한 항이 \(x_1 \lor x_2\)라는 식이라고 가정해봅시다.
이 식이 참이 되기 위해서는 둘 중 하나는 무조건 참이어야 합니다.
따라서 \(\lnot x_1 \rightarrow x_2\), \(\lnot x_2 \rightarrow x_1\)라는 식을 얻을 수 있습니다.
이 식들을 각 항에 대해서 만듭시다.
그러면 각 \(x_n\), \(\lnot x_n\)을 정점으로 하고, \(x_i \rightarrow x_j\)라는 식이 있으면 \(x_i\)에서 \(x_j\)로의 단방향 간선이 있는 그래프로 변환할 수 있습니다.
이 그래프의 어떤 정점 \(x_i\)에 대해, 이 그래프에서 \(x_i\)에서 \(\lnot x_i\)로 이동하는 경로와 \(\lnot x_i\)에서 \(x_i\)로 이동하는 경로가 둘 다 존재한다면 모순이 생기기 때문에 식을 참으로 만들 수 없음을 알 수 있습니다.
다시 말해서, 그래프를 SCC로 분할하여 \(x_i\)와 \(\lnot x_i\)가 같은 SCC에 존재한다면 모순이고, 그렇지 않다면 답이 존재합니다.
모순의 존재여부는 SCC로 알 수 있다고 하고, 모순이 없을 때 실해를 하나 찾아야 한다면 어떻게 해야 할까요?
SCC들을 위상정렬하고, 먼저 방문되는 SCC에 속하는 정점들이 최대한 거짓이 되도록 설정하면 하나의 실해를 구할 수 있습니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
|
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
ll gcd(ll a, ll b) { for (; b; a %= b, swap(a, b)); return a; }
int n, m;
vector <int> graph[20001];
vector<vector<int> > SCC;
int DFS_cnt = 1;
int DFS_num[20001];
int DFS_min[20001];
int SCC_num[200001];
int cache[20001];
vector <int> stk;
int num(int x)
{
if (x > 0) return x;
return -x + n;
}
void DFS(int v)
{
cache[v] = 1;
DFS_num[v] = DFS_min[v] = DFS_cnt++;
stk.push_back(v);
for (int nv : graph[v])
{
if (!DFS_num[nv]) DFS(nv);
if (cache[nv]) DFS_min[v] = min(DFS_min[v], DFS_min[nv]);
}
if (DFS_num[v] == DFS_min[v])
{
SCC.emplace_back();
while (true)
{
int tv = stk.back();
SCC.back().push_back(tv);
cache[tv] = 0;
stk.pop_back();
SCC_num[tv] = SCC.size() - 1;
if (tv == v) break;
}
}
}
void DFS2(int s)
{
cache[s] = 1;
for (int v : SCC[s])
{
for (int nv : graph[v])
{
int ns = SCC_num[nv];
if (cache[ns]) continue;
DFS2(ns);
}
}
stk.push_back(s);
}
int ans[20001];
int main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m;
for (int i = 0; i < m; i++)
{
int u, v; cin >> u >> v;
graph[num(-u)].push_back(num(v));
graph[num(-v)].push_back(num(u));
}
for (int i = 1; i <= 2 * n; i++)
{
if (!DFS_num[i]) DFS(i);
}
for (int i = 1; i <= n; i++)
{
if (SCC_num[i] == SCC_num[i + n])
{
cout << 0;
return 0;
}
}
cout << "1\n";
for (int i = 0; i < SCC.size(); i++)
{
if (!cache[i]) DFS2(i);
}
memset(ans, -1, sizeof ans);
while (!stk.empty())
{
int s = stk.back(); stk.pop_back();
int res = 0;
for (int v : SCC[s])
{
if (ans[v] != -1)
{
res = ans[v];
break;
}
}
for (int v : SCC[s])
{
if (v <= n) ans[v] = res, ans[v + n] = 1 - res;
else ans[v] = res, ans[v - n] = 1 - res;
}
}
for (int i = 1; i <= n; i++) cout << ans[i] << ' ';
}
|
제 그룹의 문제집에서 연습 문제들을 관리하고 있습니다.
문제집의 문제들을 보고 싶으시다면, 가입 신청을 해 주세요.
ANZ1217
무슨 내용을 넣어야 좋을까요?
www.acmicpc.net
'알고리즘 > 그래프' 카테고리의 다른 글
| 이분 매칭 (1) | 2020.07.07 |
|---|---|
| Biconnected Component (1) | 2020.06.22 |
| Euler tour technique (0) | 2020.06.15 |
| 최소 공통 조상 (0) | 2020.05.11 |
| 위상 정렬 (0) | 2020.05.10 |



