트리를 펴서 배열에 저장해봅시다.
다음과 같은 트리가 있다고 가정해봅시다. 1번 정점이 루트입니다.
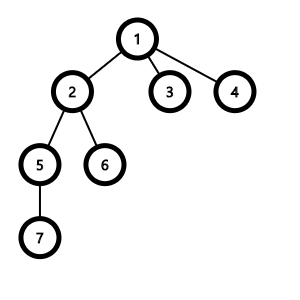
이 트리에서 루트인 1번 정점부터 시작해 DFS를 돌립니다.
그리고 각 정점이 방문되는 순서대로 번호를 다시 붙여줍시다.
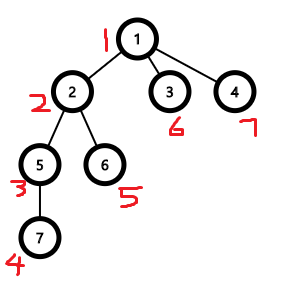
그리고 새로 붙인 번호를 인덱스로 하는 배열에 각 정점을 저장합시다.
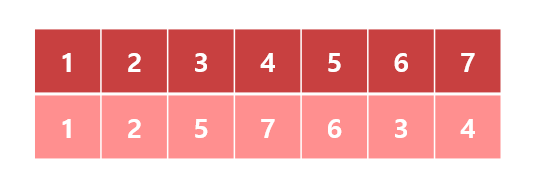
그러면 트리를 배열에 저장할 수 있게 됩니다.
방법은 매우 간단한데, 굳이 이런식으로 저장을 하는 이유가 뭘까요?
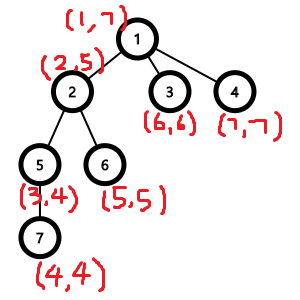
이런 식으로 트리를 저장하면, 각 정점을 루트로 하는 서브트리가 모두 하나의 구간으로 나타나게 됩니다.

1번 정점의 서브트리는 구간 \([1,7]\),
2번 정점의 서브트리는 구간 \([2,5]\),
3번 정점의 서브트리는 구간 \([6,6]\)...
이와 같이 각 서브트리를 하나의 구간으로 바꿔 생각할 수 있게 됩니다.
구간의 시작지점은 각 정점이 처음 방문 되었을 때, 끝 지점은 그 정점에서의 DFS함수가 끝났을 때의 번호를 저장함으로써 알 수 있습니다.
https://www.acmicpc.net/problem/2820
2820번: 자동차 공장
문제 상근이는 자동차를 매우 좋아한다. 자동차 공장에 취직한 상근이는 계속된 승진 끝에 드디어 사장이 되었다. 공장에는 총 N명의 직원이 있다. 상근이를 제외한 모든 직원은 한 명의 상사가
www.acmicpc.net
이를 이용한 문제를 풀어봅시다.
2가지 쿼리가 주어집니다.
1번 쿼리는 트리의 정점이 주어지고, 이 정점을 루트로 하는 서브트리에서 루트를 제외한 모든 정점에 저장된 수에 x를 더해야 합니다.
2번 쿼리는 트리의 정점이 주어지면, 이 정점에 저장된 수를 출력해야 합니다.
Euler tour technique을 이용하면 트리의 서브트리를 배열에서의 한 구간으로 나타낼 수 있으므로,
구간 갱신이 가능하고, 한 점에 저장된 값을 빠르게 알아낼 수 있는 자료구조인 세그먼트 트리를 이용할 수 있게 됩니다.
Lazy Propagation을 굳이 쓰지 않고도 풀 수 있으니 참고합시다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
|
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
ll gcd(ll a, ll b) { for (; b; a %= b, swap(a, b)); return a; }
const int N = 500010;
int n, m;
ll segTree[N]; // Fenwick Tree
void update(int i, ll x)
{
while (i <= n)
{
segTree[i] += x;
i += i & -i;
}
}
ll getVal(int i)
{
ll res = 0;
while (i)
{
res += segTree[i];
i -= i & -i;
}
return res;
}
ll money[N];
vector <int> graph[N];
pii ett[N]; // 각 정점을 루트로 하는 서브트리를 나타내는 구간을 나타낸다.
int DFS_num = 0; // 정점을 방문한 순서를 나타내는 변수
void DFS(int v, int p)
{
ett[v].first = ++DFS_num;
// 구간의 시작 인덱스
for (int nv : graph[v])
{
if (nv == p) continue;
DFS(nv, v);
}
ett[v].second = DFS_num;
// 구간의 끝 인덱스
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m;
for (int i = 1; i <= n; i++)
{
cin >> money[i];
if (i > 1)
{
int p; cin >> p;
graph[p].push_back(i);
}
}
DFS(1, 0);
for (int i = 1; i <= n; i++)
{
update(ett[i].first, money[i]);
update(ett[i].first + 1, -money[i]);
}
while (m--)
{
char c; cin >> c;
if (c == 'p')
{
int a, x; cin >> a >> x;
update(ett[a].first + 1, x);
// 자기 자신은 포함되지 않아야 하므로 1을 더해준다.
update(ett[a].second + 1, -x);
}
else
{
int a; cin >> a;
cout << getVal(ett[a].first) << '\n';
}
}
}
|
제 그룹의 문제집에서 연습 문제들을 관리하고 있습니다.
문제집의 문제들을 보고 싶으시다면, 가입 신청을 해 주세요.
ANZ1217
무슨 내용을 넣어야 좋을까요?
www.acmicpc.net
'알고리즘 > 그래프' 카테고리의 다른 글
| Biconnected Component (1) | 2020.06.22 |
|---|---|
| Strongly Connected Component (0) | 2020.06.18 |
| 최소 공통 조상 (0) | 2020.05.11 |
| 위상 정렬 (0) | 2020.05.10 |
| 최소 스패닝 트리 (0) | 2020.05.05 |



