그래프의 간선에 '용량'이라는 개념을 추가해 봅시다. 지금까지 많이 봐왔던 '비용'의 개념과는 조금 다릅니다.
어떤 간선 \(e\)가 30의 용량을 가지고 있다면, 최대 30의 유량이 흐를 수 있음을 말합니다.
용량이 있는 방향그래프에서, 시작점 \(S\)에서 끝점 \(T\)까지 흐를 수 있는 최대 유량(Maximum Flow)가 얼마인지 구하는 문제를 네트워크 유량 문제라고 합니다.
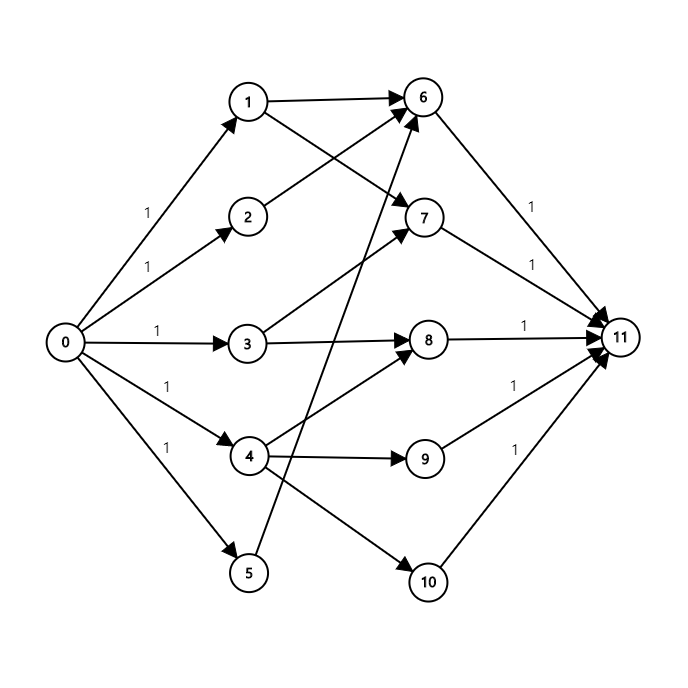
예를 들어 다음과 같은 그래프에서,

최대 유량은 60이고, 실해는 다음과 같습니다.

다양한 문제들을 유량 문제로 변환해 풀 수 있습니다.
예를 들어 이전 글에 썼던 이분 매칭의 경우, 다음과 같은 방식으로 변환하면 유량 문제로 바꿔서 풀 수도 있습니다.

https://www.acmicpc.net/problem/11378
11378번: 열혈강호 4
첫째 줄에 직원의 수 N과 일의 개수 M, 지난달에 받은 벌점의 합 K가 주어진다. (1 ≤ N, M ≤ 1,000, 1 ≤ K ≤ N) 둘째 줄부터 N개의 줄의 i번째 줄에는 i번 직원이 할 수 있는 일의 개수와 할 수 있는 �
www.acmicpc.net
직원이 \(N\)명, 해야 할 일이 \(M\)개가 있고, 각각의 일을 담당하는 사람은 1명이어야 합니다.
모든 직원은 최대 하나의 일을 할 수 있고 추가로 총 \(K\)개의 일을 더 할 수 있으므로, 문제를 다음과 같은 유량 그래프에서 최대 유량을 구하는 문제로 생각할 수 있습니다.
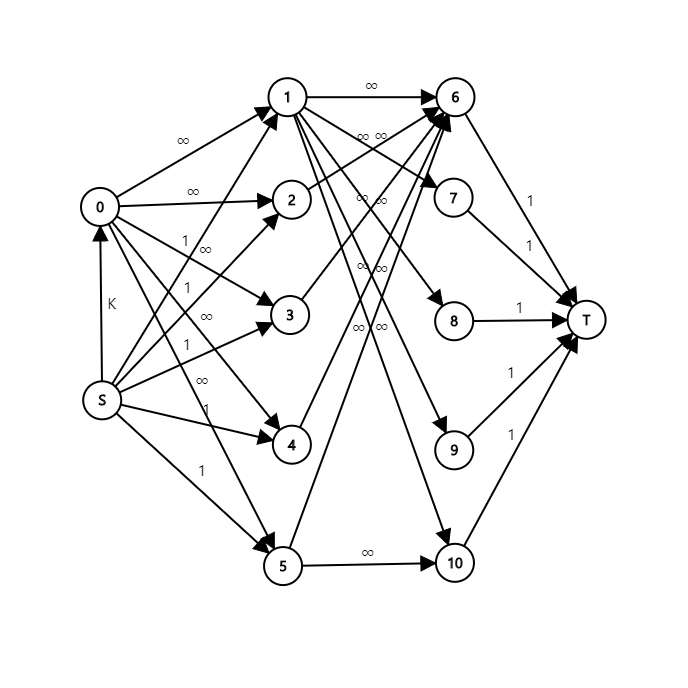
그러면 최대 유량을 구하는 방법에 대해 알아봅시다.
1. 포드-풀커슨 알고리즘(Ford-Fulkerson's Algorithm)
시작점 \(S\)에서 \(T\)까지 향하는 경로 하나를 DFS로 찾습니다.
현재 간선의 용량이 0보다 크다면 이 간선을 이용할 수 있습니다.
경로를 하나 찾았다면, 이 경로에 해당하는 간선의 용량의 최소값에 해당하는 유량 \(f\)를 흘릴 수 있게 됩니다.
따라서 답에 \(f\)를 더한 다음, 경로에 해당하는 각 간선의 용량을 \(f\)만큼 감소시켜주면 됩니다.
이 때, 각 간선의 역방향 간선에 대해서는 용량을 \(f\)만큼 증가시켜줘야 합니다.
(나중에 이 간선으로 사용한 용량을 취소할 수 있게 하기 위함입니다)
이 작업을 더 이상 유량을 흘릴 수 없을 때 까지 반복하면 됩니다.
자세한 구현 방법은 코드를 참고합시다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
|
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
ll gcd(ll a, ll b) { for (; b; a %= b, swap(a, b)); return a; }
int n, m, k;
const int S = 2001, T = 2002;
const int INF = 987654321;
const int N = 2010;
int fl[N][N];
int cache[N];
int DFS(int v, int cf) // 현재 정점, 지금까지 흐를 수 있는 유량
{
cache[v] = 1;
if (v == T) return cf;
for (int nv = 0; nv < N; nv++)
{
if (cache[nv]) continue;
if (!fl[v][nv]) continue;
int res = DFS(nv, min(cf, fl[v][nv]));
if (res)
{
// 가능한 경로를 하나 찾았다.
fl[v][nv] -= res;
fl[nv][v] += res;
return res;
}
}
return 0;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m >> k;
fl[S][0] = k;
for (int i = 1; i <= n; i++) fl[S][i] = 1, fl[0][i] = INF;
for (int i = n + 1; i <= n + m; i++) fl[i][T] = 1;
for (int i = 1; i <= n; i++)
{
int sz; cin >> sz;
for (int j = 0; j < sz; j++)
{
int w; cin >> w;
fl[i][n + w] = INF;
}
}
int ans = 0;
while (true)
{
memset(cache, 0, sizeof cache);
int res = DFS(S, INF);
if (res == 0) break;
ans += res;
}
cout << ans;
}
|
한번의 단계마다 최소 1의 유량을 추가하게 되고, 각 단계마다 \(O(E)\) DFS를 수행하므로,
총 시간 복잡도는 \(O(fE)\)입니다. (\(f\) : 최대 유량)
덧붙여 위의 코드는 인접 행렬을 사용했기 때문에 DFS의 시간복잡도가 \(O(V^2)\)지만,
인접 리스트를 사용하면 \(O(E)\)의 시간복잡도로 문제를 해결할 수 있습니다.
2. 에드몬드-카프 알고리즘(Edmonds-Karp Algorithm)
포드-풀커슨 알고리즘은 유량을 구하는 가장 간단한 알고리즘이지만,
시간복잡도가 최대 유량에 영향을 받기 때문에, 흐를 수 있는 유량의 절대값이 커지면 매우 느리게 작동하게 됩니다.
DFS로 가능한 유량을 찾을 때의 가장 큰 문제점은 \(S\)에서 \(T\)로 향하는 경로를 찾을 때 최단거리로 찾지 않기 때문에, 용량이 작은 간선을 계속 사용할 가능성이 있다는 것입니다.
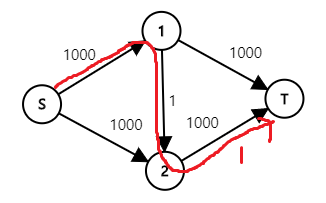


그러면 \(S\)에서 \(T\)까지의 경로를 하나 찾을 때, 최단거리로 찾기 위해 BFS를 이용해야겠다는 생각을 할 수 있습니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
|
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
ll gcd(ll a, ll b) { for (; b; a %= b, swap(a, b)); return a; }
int n, m, k;
const int S = 2001, T = 2002;
const int INF = 987654321;
const int N = 2010;
struct Node
{
int nv;
int fl;
int ridx; // 역방향 간선의 인덱스
};
vector <Node> graph[N];
int cache[N];
int par[N], pidx[N];
bool BFS() // 경로가 존재하면 true
{
memset(cache, 0, sizeof cache);
queue <int> q;
cache[S] = 1; q.push(S);
while (!q.empty())
{
int v = q.front(); q.pop();
for (int i = 0; i < graph[v].size(); i++)
{
int nv = graph[v][i].nv;
int fl = graph[v][i].fl;
if (cache[nv]) continue;
if (!fl) continue;
par[nv] = v;
pidx[nv] = i;
cache[nv] = 1;
q.push(nv);
}
}
return cache[T];
}
int getFlow(int v, int cf) // 현재 정점, 지금까지 흐를 수 있는 용량
{
if (v == S) return cf;
int pv = par[v];
int& fl = graph[pv][pidx[v]].fl;
int& rfl = graph[v][graph[pv][pidx[v]].ridx].fl;
int res = getFlow(par[v], min(cf, fl));
fl -= res;
rfl += res;
return res;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m >> k;
graph[S].push_back({ 0,k,(int)graph[0].size() });
graph[0].push_back({ S,0,(int)graph[S].size() - 1 });
for (int i = 1; i <= n; i++)
{
graph[S].push_back({ i,1,(int)graph[i].size() });
graph[i].push_back({ S,0,(int)graph[S].size() - 1 });
graph[0].push_back({ i,INF,(int)graph[i].size() });
graph[i].push_back({ 0,0,(int)graph[0].size() - 1 });
}
for (int i = n + 1; i <= n + m; i++)
{
graph[i].push_back({ T,1,(int)graph[T].size() });
graph[T].push_back({ i,0,(int)graph[i].size() - 1 });
}
for (int i = 1; i <= n; i++)
{
int sz; cin >> sz;
for (int j = 0; j < sz; j++)
{
int w; cin >> w; w += n;
graph[i].push_back({ w,INF,(int)graph[w].size() });
graph[w].push_back({ i,0,(int)graph[i].size() - 1 });
}
}
int ans = 0;
while (BFS())
{
memset(cache, 0, sizeof cache);
int res = getFlow(T, INF);
ans += res;
}
cout << ans;
}
|
인접 리스트로 구현한 코드입니다.
에드몬드-카프를 이용하면 많아도 \(VE\)번의 단계로 최대 유량을 찾을 수 있음이 증명되어 있습니다.
한 단계마다 \(O(E)\) BFS를 실행하므로, 총 시간복잡도는 \(O(VE^2)\)입니다.
3. 디닉 알고리즘(Dinic's Algorithm)
역시 대부분의 유량문제는 에드몬드-카프 알고리즘으로 해결할 수 있지만, 시간복잡도를 더 줄일 수 있습니다.
이분 매칭에서의 홉크로프트-카프와 같이, BFS로 시작점에서 각 정점까지의 거리를 계산합시다.
그 후 포드-풀커슨과 같은 방식으로 DFS를 이용해 유량을 흘려주는데, 흘릴 수 있는 유량을 모두 찾아 한번에 흘려줍니다.
이 때, 한 정점에서 다른 정점으로 유량을 흘리려면 BFS로 계산한 거리의 차이가 1이어야 합니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
|
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
ll gcd(ll a, ll b) { for (; b; a %= b, swap(a, b)); return a; }
int n, m, k;
const int S = 2001, T = 2002;
const int INF = 987654321;
const int N = 2010;
struct Node
{
int nv;
int fl;
int ridx; // 역방향 간선의 인덱스
};
vector <Node> graph[N];
int dist[N];
bool BFS() // 경로가 존재하면 true
{
memset(dist, -1, sizeof dist);
queue <int> q;
dist[S] = 0; q.push(S);
while (!q.empty())
{
int v = q.front(); q.pop();
for (int i = 0; i < graph[v].size(); i++)
{
int nv = graph[v][i].nv;
int fl = graph[v][i].fl;
if (dist[nv] != -1) continue;
if (!fl) continue;
dist[nv] = dist[v] + 1;
q.push(nv);
}
}
return dist[T] != -1;
}
int idx[N]; // DFS에서 한 번 쓰지 않겠다고 정한 간선은 더 이상 쓸 일이 없다.
int DFS(int v, int cf) // 현재 정점, 지금까지 흐를 수 있는 용량
{
if (v == T) return cf;
for (int& i = idx[v]; i < graph[v].size(); i++)
{
int nv = graph[v][i].nv;
int& fl = graph[v][i].fl;
int& rfl = graph[nv][graph[v][i].ridx].fl;
if (fl == 0) continue;
if (dist[v] + 1 != dist[nv]) continue;
int res = DFS(nv, min(cf, fl));
if (res)
{
fl -= res;
rfl += res;
return res;
}
}
return 0;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m >> k;
graph[S].push_back({ 0,k,(int)graph[0].size() });
graph[0].push_back({ S,0,(int)graph[S].size() - 1 });
for (int i = 1; i <= n; i++)
{
graph[S].push_back({ i,1,(int)graph[i].size() });
graph[i].push_back({ S,0,(int)graph[S].size() - 1 });
graph[0].push_back({ i,INF,(int)graph[i].size() });
graph[i].push_back({ 0,0,(int)graph[0].size() - 1 });
}
for (int i = n + 1; i <= n + m; i++)
{
graph[i].push_back({ T,1,(int)graph[T].size() });
graph[T].push_back({ i,0,(int)graph[i].size() - 1 });
}
for (int i = 1; i <= n; i++)
{
int sz; cin >> sz;
for (int j = 0; j < sz; j++)
{
int w; cin >> w; w += n;
graph[i].push_back({ w,INF,(int)graph[w].size() });
graph[w].push_back({ i,0,(int)graph[i].size() - 1 });
}
}
int ans = 0;
while (BFS())
{
memset(idx, 0, sizeof idx);
while (true)
{
int res = DFS(S, INF);
if (res == 0) break;
ans += res;
}
}
cout << ans;
}
|
시간복잡도는 \(O(V^2E)\)입니다.
최대 유량 최소 컷(Maximum Flow Minimum Cut)
유량 문제로 풀 수 있는 문제 중 최소 컷 문제가 있습니다.
가중치가 있는 그래프가 주어집니다.
이 그래프에서 임의의 두 정점을 분리하려고 합니다. (같은 컴포넌트에 있지 않도록 해야 합니다.)
그러기 위해서 간선을 끊어내야 하는데, 각 간선을 끊는 비용이 간선의 가중치라고 합시다.
이 때 두 정점을 분리하는데 필요한 최소 비용을 구하는 문제를 최소 컷 문제라고 합니다.
두 정점을 \(S, T\)로 설정하고, 가중치를 용량으로 설정했을 때,
\(S\)에서 \(T\)까지 흐르는 최대 유량은 위 문제의 최소 컷과 같습니다.
제 그룹의 문제집에서 연습 문제들을 관리하고 있습니다.
문제집의 문제들을 보고 싶으시다면, 가입 신청을 해 주세요.
ANZ1217
무슨 내용을 넣어야 좋을까요?
www.acmicpc.net
'알고리즘 > 그래프' 카테고리의 다른 글
| HLD (1) | 2021.08.25 |
|---|---|
| Minimum Cost Maximum Flow (0) | 2020.07.14 |
| 이분 매칭 (1) | 2020.07.07 |
| Biconnected Component (1) | 2020.06.22 |
| Strongly Connected Component (0) | 2020.06.18 |



