만약 그래프의 간선에 비용과 용량이 모두 존재하면 어떨까요?
간선에 1의 용량을 흘릴 때마다 그 간선에 주어진 비용이 드는 그래프를 생각할 수 있습니다.
용량과 비용이 있는 방향그래프에서, 시작점 \(S\)에서 끝점 \(T\)까지 흐를 수 있는 최대 용량을 구하되, 그 때의 비용을 최소로 만드는 문제를 MCMF(Minimum Cost Maximum Flow) 문제라고 합니다.
예를 들어 다음과 같은 그래프에서,
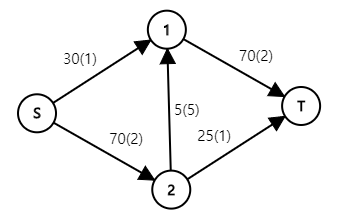
최대 유량은 60, 그 때의 최소 비용은 210이고, 실해는 다음과 같습니다.

https://www.acmicpc.net/problem/11408
11408번: 열혈강호 5
강호네 회사에는 직원이 N명이 있고, 해야 할 일이 M개가 있다. 직원은 1번부터 N번까지 번호가 매겨져 있고, 일은 1번부터 M번까지 번호가 매겨져 있다. 각 직원은 한 개의 일만 할 수 있고, 각각��
www.acmicpc.net
직원이 \(N\)명, 해야 할 일이 \(M\)개가 있고, 각 직원은 하나의 일만 할 수 있으며, 각 일은 한 명만이 담당할 수 있다고 합니다.
각 직원이 할 수 있는 일과 그 때 지불해야 하는 월급이 주어질 때, 최대 할 수 있는 일의 개수와 그 때 지불해야 하는 월급의 최소값을 구하라고 합니다.
문제를 다음과 같은 그래프에서의 MCMF문제로 생각하고 풀 수 있습니다.
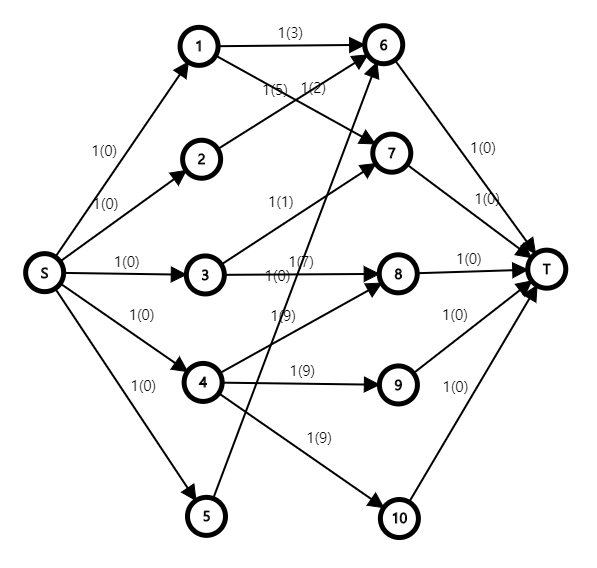
MCMF를 구하는 방법은 생각보다 간단합니다.
시작점에서 시작해 끝 점까지의 최단거리를 구합시다. 비용을 가중치로 생각합니다.
그 다음은 기존의 최대 유량을 구할 때와 비슷한데, 현재 그래프에서 시작점에서 끝점까지의 최단거리에 해당하는 간선들을 이용해 유량을 흘립니다. 그러면 현재 가능한 최소 비용으로 흘릴 수 있는 유량을 모두 흘린 것이 됩니다.
이를 더 이상 유량을 흘리지 못할 때까지 반복하면 됩니다.
최단거리를 구할 때는 어떤 알고리즘을 이용해야 할까요?
우리가 최대 유량을 구할 때, 어떤 간선을 이용해 유량을 흘렸다면 이 간선의 용량은 줄이고, 반대 방향으로의 간선을 이용하는 용량은 늘렸습니다.
그렇다면 반대 방향으로의 간선의 비용은 어떻게 될까요?
반대 방향으로의 간선을 이용한다는 것은 이전에 흘린 유량을 취소한다는 말이므로, 원래 간선의 비용이 \(c\)였다면, 역방향 간선의 비용은 \(-c\)가 됩니다.
따라서 음수 가중치가 존재하는 그래프에서의 최단거리를 구할 수 있는 알고리즘을 사용해야 합니다.
벨만-포드나 SPFA를 사용할 수 있고, 아무래도 평균적으로 더 빠른 SPFA를 사용하는게 좋을 것입니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
|
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
ll gcd(ll a, ll b) { for (; b; a %= b, swap(a, b)); return a; }
const int N = 805;
const int S = 0;
const int T = 801;
const int INF = 987654321;
struct Node
{
int nv;
int fl;
int ct; // 비용
int ridx; // 역방향 간선의 인덱스
};
int n, m;
vector <Node> graph[N];
int dist[N];
bool inQ[N];
int par[N], pidx[N];
bool SPFA()
{
fill(dist, dist + N, INF);
queue <int> q;
dist[S] = 0, q.push(S), inQ[S] = 1;
while (!q.empty())
{
int v = q.front(); q.pop();
inQ[v] = 0;
for (int i = 0; i < graph[v].size(); i++)
{
auto it = graph[v][i];
int nv = it.nv;
int d = it.ct;
int fl = it.fl;
if (fl == 0) continue;
if (dist[nv] > dist[v] + d)
{
par[nv] = v;
pidx[nv] = i;
dist[nv] = dist[v] + d;
if (!inQ[nv])
{
q.push(nv);
inQ[nv] = 1;
}
}
}
}
return dist[T] != INF;
}
pii solve(int v, int cf) // {최대 용량, 용량 1당 비용}을 반환
{
if (v == S) return { cf, 0 };
int pv = par[v];
int ct = graph[pv][pidx[v]].ct;
int& fl = graph[pv][pidx[v]].fl;
int& rfl = graph[v][graph[pv][pidx[v]].ridx].fl;
pii res = solve(pv, min(cf, fl));
fl -= res.first;
rfl += res.first;
return { res.first, res.second + ct };
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m;
for (int i = 1; i <= n; i++)
{
graph[S].push_back({ i,1,0,(int)graph[i].size() });
graph[i].push_back({ S,0,0,(int)graph[S].size() - 1 });
}
for (int i = 1; i <= n; i++)
{
int sz; cin >> sz;
while (sz--)
{
int nv, ct; cin >> nv >> ct;
nv += n;
graph[i].push_back({ nv,1,ct,(int)graph[nv].size() });
graph[nv].push_back({ i,0,-ct,(int)graph[i].size() - 1 });
}
}
for (int i = n + 1; i <= n + m; i++)
{
graph[i].push_back({ T,1,0,(int)graph[T].size() });
graph[T].push_back({ i,0,0,(int)graph[i].size() - 1 });
}
int fl = 0, ct = 0;
while (SPFA())
{
pii res = solve(T, INF);
fl += res.first;
ct += res.first * res.second;
}
cout << fl << '\n' << ct;
}
|
한번의 단계마다 최소 1의 유량이 흐를 수 있고, 각 단계마다 \(O(VE)\) SPFA를 수행하므로,
총 시간복잡도는 \(O(fVE)\)입니다. (\(f\) : 최대 유량)
제 그룹의 문제집에서 연습 문제들을 관리하고 있습니다.
문제집의 문제들을 보고 싶으시다면, 가입 신청을 해 주세요.
ANZ1217
무슨 내용을 넣어야 좋을까요?
www.acmicpc.net
'알고리즘 > 그래프' 카테고리의 다른 글
| Centroid Decomposition (0) | 2021.10.13 |
|---|---|
| HLD (1) | 2021.08.25 |
| 네트워크 유량 (0) | 2020.07.10 |
| 이분 매칭 (1) | 2020.07.07 |
| Biconnected Component (1) | 2020.06.22 |



