유니온 파인드 (Union-Find Disjoint Set)은 교집합이 없는 서로소 집합들을 다루는 자료구조입니다.
유니온 파인드를 이용하면 서로소 집합들을 서로 합치거나(Union), 특정 원소가 어떤 집합에 속해있는지(Find) 알아내는 연산을 매우 효율적으로 할 수 있습니다.
유니온 파인드에서의 한 집합은 하나의 대표값(원소)로 표시하며, 그 집합에 포함된 다른 원소들은 대표원소로 가는 경로가 존재하는 트리 형태로 저장되게 됩니다.
예를 들어봅시다.
초기에 모든 원소들은 자기 자신을 대표원소로 가지는 크기 1인 집합에 속해 있습니다.

$$\{1\},\{2\},\{3\},\{4\},\{5\},\{6\}$$
여기에서 2번 집합과 3번 집합을 합치는 연산을 해봅시다.
합칠 때는 두 집합의 대표값중 하나를 합쳐진 집합의 대표값으로 설정하고, 나머지 대표값을 자식으로 연결시켜주면 됩니다.
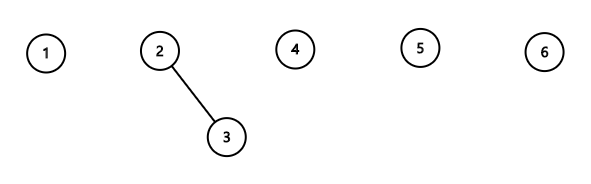
$$\{1\},\{2,3\},\{4\},\{5\},\{6\}$$
같은 방식으로 4번과 6번 집합도 합쳐봅시다.

$$\{1\},\{2,3\},\{4,6\},\{5\}$$
여기에서 3번 원소가 포함된 집합과, 6번 원소가 포함된 집합을 합쳐봅시다.
집합 \(\{2,3\}\)의 대표값은 \(2\)이고, 집합 \(\{4,6\}\)의 대표값은 4이므로,
\(2\)와 \(4\)중 하나를 새로운 집합의 대표값으로 하고, 나머지를 자식으로 이어주면 됩니다.

$$\{1\},\{2,3,4,6\},\{5\}$$
이제 각 원소가 어떤 집합에 속하는지 알고 싶다면, 각 원소의 대표값을 알아내기만 하면 됩니다.
합치는 연산이 일어날 때마다 각 원소의 부모를 갱신해줍시다.
원소의 대표값을 찾을 때에는 부모가 없는 원소(트리의 루트)가 나올 때까지 트리를 거슬러 올라가면 찾을 수 있게 됩니다.
위를 구현한 코드가 다음과 같습니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
const int N = 100001;
int par[N]; // 원소의 현재 부모 (0이면 없음)
int getPar(int a) // a가 포함된 집합의 대표값을 반환한다.
{
if (par[a] == 0) return a;
// 만약 a의 부모가 없다면 a가 대표값이다.
else return getPar(par[a]);
// 그렇지 않다면, 부모의 부모를 찾는다.
}
void merge(int a, int b) // 두 원소가 포함된 집합을 합친다.
{
a = getPar(a);
b = getPar(b);
// 각 원소가 포함된 집합의 대표값으로 바꿔준다.
if (a == b) return;
// 이미 같은 집합이라면 무시한다.
par[a] = b;
// 한 집합을 다른 집합의 자식으로 이어준다.
}
|
하지만 이 코드는 다음과 같은 상황에서 느리게 작동하게 됩니다.

두 집합을 합치는 과정에서, 운이 좋지 않다면 위와 같이 일자로 이어진 트리 형태로 연결될 수 있게 됩니다.
만약 원소가 더 많다면 부모를 찾는 연산이 최악의 경우 \(O(n)\)으로 너무 느리게 작동할 겁니다.
이 부분을 최적화 해봅시다.
만약 트리의 높이가 다른 두 집합을 합칠 때, 어떤 원소를 대표값으로 하는 것이 더 유리할까요?
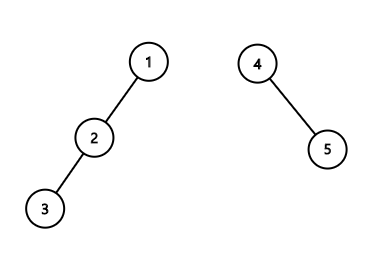
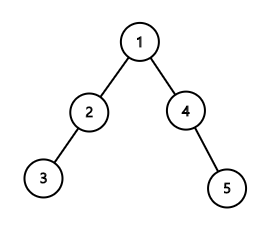
잘 생각해보면 두 집합을 합친다고 할 때, 높이가 더 높은 집합을 대표로 하는 것이 더 유리함을 알 수 있습니다.
높이가 낮은 집합을 대표로 한다면 트리의 전체 높이가 더 높아지기 때문에, 대표값을 찾는 연산을 하는데 더 많은 시간이 걸리기 때문입니다.
따라서 각 집합을 나타내는 트리의 높이를 저장한 다음, 합칠 때 더 높은 트리를 가지는 집합을 대표로 하도록 코드를 작성해봅시다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
const int N = 100001;
int par[N]; // 원소의 현재 부모 (0이면 없음)
int height[N]; // 각 원소를 루트로 하는 트리의 높이
int getPar(int a) // a가 포함된 집합의 대표값을 반환한다.
{
if (par[a] == 0) return a;
// 만약 a의 부모가 없다면 a가 대표값이다.
else return getPar(par[a]);
// 그렇지 않다면, 부모의 부모를 찾는다.
}
void merge(int a, int b) // 두 원소가 포함된 집합을 합친다.
{
a = getPar(a);
b = getPar(b);
// 각 원소가 포함된 집합의 대표값으로 바꿔준다.
if (a == b) return;
// 이미 같은 집합이라면 무시한다.
if (height[a] > height[b]) // a가 더 높이가 높다면
{
par[b] = a;
// b를 a의 자식으로 한다.
}
else // 그렇지 않다면
{
par[a] = b;
// a를 b의 자식으로 한다.
if (height[a] == height[b]) // 만약 높이가 서로 같다면
{
height[b]++;
// b의 높이가 1 증가한다.
}
}
}
|
이 정도 최적화만으로도 각 원소의 대표값을 찾는데 \(O(\log n)\)의 시간이 걸리므로 충분히 훌륭하지만, 한 가지 최적화가 더 가능합니다.
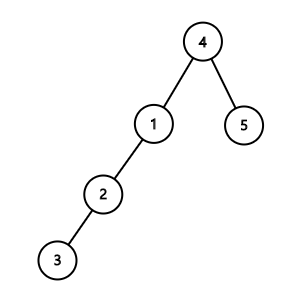
대표값을 찾는 연산을 할 때, 경로 상에 있는 모든 원소들을 대표값에 직접 연결되도록 바꿔준다면 시간을 더 줄일 수 있습니다.
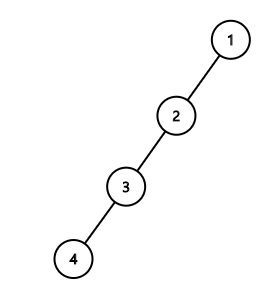

위의 왼쪽 트리에서, 4의 대표값을 찾는데 3, 2, 1을 거쳐 대표값이 1임을 알아냈습니다.
그 다음 2, 3, 4의 부모를 대표값인 1로 직접 연결되도록 경로압축을 해주면 다음 연산을 할 때 실행속도가 빨라지게 됩니다.
위의 최적화까지 했을 때 대표값을 찾는 연산의 시간복잡도는 사실상 상수라고 생각해도 무방합니다.
https://www.acmicpc.net/problem/1717
1717번: 집합의 표현
첫째 줄에 n(1≤n≤1,000,000), m(1≤m≤100,000)이 주어진다. m은 입력으로 주어지는 연산의 개수이다. 다음 m개의 줄에는 각각의 연산이 주어진다. 합집합은 0 a b의 형태로 입력이 주어진다. 이는 a가 포함되어 있는 집합과, b가 포함되어 있는 집합을 합친다는 의미이다. 두 원소가 같은 집합에 포함되어 있는지를 확인하는 연산은 1 a b의 형태로 입력이 주어진다. 이는 a와 b가 같은 집합에 포함되어 있는지를 확인하는 연산이다. a
www.acmicpc.net
위의 모든 최적화를 포함해 작성한 코드입니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
|
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 1000001;
int n, m;
int par[N]; // 원소의 현재 부모 (-1 이면 없음)
int height[N]; // 각 원소를 루트로 하는 트리의 높이
int getPar(int a) // a가 포함된 집합의 대표값을 반환한다.
{
if (par[a] == -1) return a;
// 만약 a의 부모가 없다면 a가 대표값이다.
else return par[a] = getPar(par[a]);
// 그렇지 않다면, 부모의 부모를 찾는다.
// 동시에 경로압축을 해준다.
}
void merge(int a, int b) // 두 원소가 포함된 집합을 합친다.
{
a = getPar(a);
b = getPar(b);
// 각 원소가 포함된 집합의 대표값으로 바꿔준다.
if (a == b) return;
// 이미 같은 집합이라면 무시한다.
if (height[a] > height[b]) // a가 더 높이가 높다면
{
par[b] = a;
// b를 a의 자식으로 한다.
}
else // 그렇지 않다면
{
par[a] = b;
// a를 b의 자식으로 한다.
if (height[a] == height[b]) // 만약 높이가 서로 같다면
{
height[b]++;
// b의 높이가 1 증가한다.
}
}
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
memset(par, -1, sizeof par);
cin >> n >> m;
while (m--)
{
int q, a, b;
cin >> q >> a >> b;
if (q == 0)
{
merge(a, b);
}
else
{
if (getPar(a) == getPar(b)) cout << "YES\n";
else cout << "NO\n";
}
}
}
|
제 그룹의 문제집에서 연습 문제들을 관리하고 있습니다.
문제집의 문제들을 보고 싶으시다면, 가입 신청을 해 주세요.
https://www.acmicpc.net/group/7712
ANZ1217
무슨 내용을 넣어야 좋을까요?
www.acmicpc.net
'알고리즘 > 자료구조' 카테고리의 다른 글
| 세그먼트 트리 응용 (0) | 2021.08.02 |
|---|---|
| 세그먼트 트리 with Lazy propagation (1) | 2020.06.01 |
| 세그먼트 트리 (0) | 2020.05.15 |
| 내장 라이브러리가 있는 자료 구조 (0) | 2020.04.28 |

