
Vestigium
Code Jam - Google’s Coding Competitions
Put your coding skills to the test as you work your way through multiple rounds of algorithmic coding puzzles for the title of Code Jam Champ and 15,000 USD.
codingcompetitions.withgoogle.com
\(N\)크기의 라틴 방진이 주어진다.
이 라틴방진의 왼쪽 위부터 오른쪽 아래까지 이어지는 대각선에 있는 수들의 합과
겹치는 수가 있는 행의 개수, 그리고 겹치는 수가 있는 열의 개수를 각각 출력하면 된다.
\(1 \le M_{i,j} \le N\)임이 주어졌으므로,
한 행(또는 열)의 수들을 모두 set에 저장했을 때 set의 크기가 \(N\)이 아니라면 겹치는 수가 있다는 것을 알 수 있다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
ll gcd(ll a, ll b) { for (; b; a %= b, swap(a, b)); return a; }
int n;
int m[101][101];
int main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
int T; cin >> T;
for (int t = 1; t <= T; t++)
{
cin >> n;
for (int i = 0; i < n; i++) for (int j = 0; j < n; j++) cin >> m[i][j];
int k = 0, r = 0, c = 0;
for (int i = 0; i < n; i++) k += m[i][i];
for (int i = 0; i < n; i++)
{
set <int> s;
for (int j = 0; j < n; j++) s.insert(m[i][j]);
if (s.size() < n) r++;
}
for (int j = 0; j < n; j++)
{
set <int> s;
for (int i = 0; i < n; i++) s.insert(m[i][j]);
if (s.size() < n) c++;
}
cout << "Case #" << t << ": " << k << ' ' << r << ' ' << c << '\n';
}
}
|
Nesting Depth
Code Jam - Google’s Coding Competitions
Put your coding skills to the test as you work your way through multiple rounds of algorithmic coding puzzles for the title of Code Jam Champ and 15,000 USD.
codingcompetitions.withgoogle.com
숫자로 이루어진 문자열 \(S\)가 주어진다.
각 숫자를 숫자 개수만큼의 괄호 쌍으로 둘러 싸려고 하는데, 한 괄호 쌍으로 여러개의 숫자를 둘러싸는 것도 가능하다.
이 규칙을 이용해 만든 (숫자와 괄호로 이루어진) 새로운 문자열들 중 가장 길이가 짧은 것을 출력해야 한다.
인접해있는 두 숫자에 대하여, \(S_i < S_{i+1}\)라면 \(S_{i+1}-S_i\)개의 여는 괄호 '(' 를,
\(S_i > S_{i+1}\)라면 \(S_i-S_{i+1}\)개의 닫는 괄호 ')' 를 추가하면 된다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
ll gcd(ll a, ll b) { for (; b; a %= b, swap(a, b)); return a; }
int main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
int T; cin >> T;
for (int t = 1; t <= T; t++)
{
string s; cin >> s;
int stk = 0;
string ans;
for (auto c : s)
{
int num = c - '0';
if (num > stk) for (int i = 0; i < num - stk; i++)
ans += '(';
if (num < stk) for (int i = 0; i < stk - num; i++)
ans += ')';
stk = num;
ans += c;
}
for (int i = 0; i < stk; i++) ans += ')';
cout << "Case #" << t << ": " << ans << '\n';
}
}
|
Parenting Partnering Returns
Code Jam - Google’s Coding Competitions
Put your coding skills to the test as you work your way through multiple rounds of algorithmic coding puzzles for the title of Code Jam Champ and 15,000 USD.
codingcompetitions.withgoogle.com
\(N\)개의 일이 주어진다. 각 일의 시작 시간과 끝 시간이 주어진다.
두 사람이 이 일들을 처리하려고 하는데, 한 사람이 동시에 2가지 일을 할 수는 없다.
하지만 한 가지 일이 끝남과 동시에 다른 일을 시작하는 것은 가능하다.
이 때, 두 사람이 모든 일을 처리하는게 가능한지 알아내야 한다.
가능하다면, 그 방법을 출력한다.
모든 일들을 시작 시간순으로 정렬한 다음, 차례대로 다음과 같이 배분하면 된다.
1. 두 명 모두 현재 일을 하고 있지 않다면, 둘 중 아무나 배정한다.
2. 한 명은 일을 하고 있고 한 명은 일을 하고 있지 않다면, 일을 안 하고 있는 사람에게 배정한다.
3. 둘다 일을 하는 중이라면, 불가능하다.
실제 해를 출력할 때는 정렬한 순서가 아니라 원래 입력이 들어온 일 순서대로 출력해야 함에 주의하자.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
|
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
ll gcd(ll a, ll b) { for (; b; a %= b, swap(a, b)); return a; }
int n;
pair<pii, int> w[1001];
char ans[1001];
int main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
int T; cin >> T;
for (int t = 1; t <= T; t++)
{
cin >> n;
for (int i = 0; i < n; i++)
cin >> w[i].first.first >> w[i].first.second, w[i].second = i;
sort(w, w + n);
bool valid = true;
int c = -1, j = -1;
for (int i = 0; i < n; i++)
{
if (c != -1 && c <= w[i].first.first) c = -1;
if (j != -1 && j <= w[i].first.first) j = -1;
if (c == -1) ans[w[i].second] = 'C', c = w[i].first.second;
else if (j == -1) ans[w[i].second] = 'J', j = w[i].first.second;
else
{
valid = false;
break;
}
}
ans[n] = 0;
cout << "Case #" << t << ": ";
if (!valid) cout << "IMPOSSIBLE\n";
else cout << ans << '\n';
}
}
|
ESAb ATAd
Code Jam - Google’s Coding Competitions
Put your coding skills to the test as you work your way through multiple rounds of algorithmic coding puzzles for the title of Code Jam Champ and 15,000 USD.
codingcompetitions.withgoogle.com
\(B\)개의 비트로 이루어진 배열이 컴퓨터에 저장되어 있다.
이 컴퓨터에 \(i\)번째 비트가 뭔지 질문하는 것을 반복해서 저장되어 있는 정보가 뭔지 복원해내려고 한다.
그런데 이 컴퓨터는 조금 불안정해서, 1번째, 11번째, 21번째... 질문이 들어오면 저장된 정보가 다음과 같이 바뀌게 된다.
25% 확률로, 바뀌지 않는다.
25% 확률로, 모든 비트가 반전된다. 0은 1로 바뀌고, 1은 0으로 바뀐다.
25% 확률로, 저장된 배열이 뒤집힌다.
25% 확률로, 배열이 뒤집히고 비트도 반전된다.
이 때, 최대 150번의 쿼리로 현재 저장되어 있는 배열의 정보를 알아내야 한다.
(당연하게도 원본은 알 수 없다. 첫번째 쿼리가 들어오자마자 변화가 일어나기 때문이다.)
먼저 \(i\)번째 비트가 뭔지 질문 하고나서, \(n+1-i\)번째 비트가 뭔지도 같이 질문할 것이다.
이런식으로 배열이 뒤집혔을 때 서로 위치가 바뀌는 비트들을 세트로 받으면서, 다음 조건에 맞는 2세트의 비트를 저장해두자.
1. 뒤집혔을 때 서로 위치가 바뀌면서 같은 비트 1세트 // (0, 0) or (1, 1)
2. 뒤집혔을 때 서로 위치가 바뀌면서 다른 비트 1세트 // (0, 1) or (1, 0)
그럼 \(10n+1\)번째 쿼리에서 배열이 바뀌었을 때 어떤 변화가 일어났는지 이 2세트의 비트를 검사해서 알 수 있다.
1번 세트의 비트 하나를 검사했는데, 원래 저장되어 있던 비트와 다르다면 반전이 일어났다는 뜻이다. (뒤집혀도 같기 때문에)
반전이 일어났다면 저장되어 있는 비트를 반전시켜 주면 된다. 그 후에,
2번 세트의 비트 하나를 검사했는데, 원래 저장되어 있던 비트와 다르다면 배열이 뒤집혔다는 뜻이다.
역시 뒤집힘이 일어났다면 저장되어 있는 비트를 뒤집어 주면 된다.
그러면 변화 없이 한 번에 할 수 있는 10개의 쿼리 중에 2번은 변화 판정, 8번은 실제 배열 복원에 쓸 수 있게 되고,
\(B=100\)일 때 최대 124번의 쿼리로 배열을 복원할 수 있다.
만약 1번이나 2번 조건에 만족하는 세트가 없어도 상관없다.
1번 세트를 만족하는 두 비트가 없다면, 비트 반전과 뒤집힘의 결과가 같은 배열이다.
2번 세트를 만족하는 두 비트가 없다면, 뒤집혀도 배열이 바뀌지 않는다. (팰린드롬이다.)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
|
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
ll gcd(ll a, ll b) { for (; b; a %= b, swap(a, b)); return a; }
int main()
{
int T, B; cin >> T >> B;
for (int t = 1; t <= T; t++)
{
vector <int> f, b;
int same_idx = -1;
int same_value = 0;
int different_idx = -1;
int different_value = 0;
int res;
int query = 1;
int idx = 1;
while (idx <= B / 2)
{
if (query % 10 == 1)
{
if (same_idx != -1)
{
cout << same_idx << endl;
cin >> res;
if (same_value != res)
{
for (auto& it : f) it = 1 - it;
for (auto& it : b) it = 1 - it;
same_value = 1 - same_value;
different_value = 1 - different_value;
}
}
else
{
cout << 1 << endl;
cin >> res;
}
if (different_idx != -1)
{
cout << different_idx << endl;
cin >> res;
if (different_value != res)
{
swap(f, b);
different_value = f[different_idx - 1];
}
}
else
{
cout << 1 << endl;
cin >> res;
}
query += 2;
}
cout << idx << endl;
cin >> res;
f.push_back(res);
cout << B - idx + 1 << endl;
cin >> res;
b.push_back(res);
if (f.back() == b.back())
same_idx = idx, same_value = f.back();
else
different_idx = idx, different_value = f.back();
query += 2;
idx++;
}
for (auto it : f) cout << it;
reverse(b.begin(), b.end());
for (auto it : b) cout << it;
cout << endl;
char judge; cin >> judge;
if (judge == 'N') return 0;
}
}
|
Indicium
Code Jam - Google’s Coding Competitions
Put your coding skills to the test as you work your way through multiple rounds of algorithmic coding puzzles for the title of Code Jam Champ and 15,000 USD.
codingcompetitions.withgoogle.com
수 \(N\)과 \(K\)가 주어진다.
왼쪽 위부터 오른쪽 아래까지 이어지는 대각선에 있는 수들의 합이 \(K\)인 \(N\)차 라틴 방진을 출력해야 한다.
\(N\)이 \(5\)이하인 경우는 총 44가지이다. 충분히 적당히 만들어 볼 수 있는 양이므로, 직접 만들어보면 된다.
그러니 \(N\)이 5보다 큰 경우에 대해 생각해보자.
대각선에 있는 수들을 만들 때, 수 3개만 이용하도록 조건을 한정해서 만들어보자.
\(A \times (N-2) + B + C = K\)
그럼 다음과 같이 3가지의 경우로 나눠지게 된다.
1. \(A = B = C\)
이 경우 대각선에 A로 전부 채워 놓은다음 나머지 수로 이루어진 순열을 1칸씩 shift해서 채워넣으면 된다.
가장 간단한 경우이다.

2. \(A \ne B \ne C\)
라틴 방진은 이런 모양이 될 것이다.
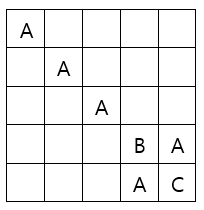
그러면 A의 이전 원소가 B이면서, A의 다음 원소가 C인 순열을 하나 만들 수 있게 된다.
이 순열을 역시 A의 위치에 맞춰 적당히 shift해서 채워 넣으면 된다.
ex) 순열이 B-A-C-D-E 일 경우

3. \(A \ne B = C\)
A와 B위치를 정해놓으면 다음과 같이 된다.
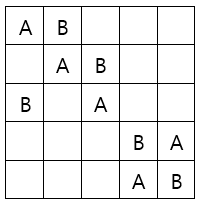
그 후 남은 수들을 모순이 없도록 적당히 채우면 답이 된다.
수들을 채울 때, 이분매칭을 이용하거나 적당한 규칙을 만들어서 채울 수 있는데,
본인은 노트에 복잡하고 더러운 규칙을 하나 찾아내서 쓴 다음 그대로 코드로 옮겼다.
이런 방식으로도 문제없이 답을 만들 수 있는 이유는 홀의 정리 때문이라고 한다.
+ \(A = B \ne C\)의 경우에는 만드는 것이 불가능하다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
|
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
ll gcd(ll a, ll b) { for (; b; a %= b, swap(a, b)); return a; }
int n, k;
int ans[51][51];
void makeLatin(int i, int j, int k)
{
vector <int> pm;
pm.push_back(i);
pm.push_back(k);
for (int x = 1; x <= n; x++)
{
if (x == i || x == j || x == k) continue;
pm.push_back(x);
}
pm.push_back(j);
for (int x = 0; x < n - 2; x++)
{
for (int y = 0; y < n; y++)
{
ans[x][(y + x) % n] = pm[y];
}
}
for (int y = 0; y < n; y++)
{
ans[n - 2][(y + n - 2) % n] = pm[(y + n - 1) % n];
}
for (int y = 0; y < n; y++)
{
ans[n - 1][(y + n - 1) % n] = pm[(y + 1) % n];
}
}
void makeLatin2(int i, int j)
{
for (int x = 0; x < n - 2; x++)
{
ans[x][x] = i;
if (x != n - 3) ans[x][x + 1] = j;
else ans[x][0] = j;
}
ans[n - 2][n - 2] = j;
ans[n - 2][n - 1] = i;
ans[n - 1][n - 2] = i;
ans[n - 1][n - 1] = j;
vector <int> pm;
for (int x = 1; x <= n; x++)
{
if (x == i || x == j) continue;
pm.push_back(x);
}
for (int x = 0; x < n - 3; x++)
{
for (int y = 0; y < n - 2; y++)
{
ans[x][(x + y + 2) % n] = pm[y];
}
}
ans[n - 3][n - 2] = ans[0][n - 1];
ans[n - 3][n - 1] = ans[n - 4][n - 2];
int hasNum[51] = { 0, };
for (int x = 0; x < 4; x++)
{
int num = ans[n - 3][(n - x) % n];
hasNum[num] = 1;
}
pm.clear();
for (int i = 1; i <= n; i++)
{
if (hasNum[i] == 0) pm.push_back(i);
}
for (int x = 1; x < n - 3; x++)
{
ans[n - 3][x] = pm[x - 1];
}
for (int x = 0; x < n - 2; x++)
{
memset(hasNum, 0, sizeof hasNum);
for (int y = 0; y < n - 2; y++)
{
int num = ans[y][x];
hasNum[num] = 1;
}
for (int z = 1; z <= n; z++)
{
if (hasNum[z]) continue;
bool flag = false;
for (int u = 0; u < x; u++)
{
if (z == ans[n - 2][u])
{
flag = true;
break;
}
}
if (flag) continue;
ans[n - 2][x] = z;
hasNum[z] = 1;
break;
}
for (int z = 1; z <= n; z++)
{
if (hasNum[z]) continue;
ans[n - 1][x] = z;
hasNum[z] = 1;
break;
}
}
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
int T; cin >> T;
for (int t = 1; t <= T; t++)
{
cin >> n >> k;
bool valid = false;
if (k % n == 0)
{
valid = true;
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
ans[i][(j + i) % n] = (k / n + j - 1) % n + 1;
}
}
if (valid)
{
cout << "Case #" << t << ": POSSIBLE\n";
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++) cout << ans[i][j] << ' ';
cout << '\n';
}
continue;
}
if (n >= 4)
{
for (int i = 1; i <= n; i++)
{
if (valid) break;
int rm = k - i * (n - 2);
for (int j = 1; j <= n; j++)
{
int k = rm - j;
if (k < 1 || k > n) continue;
if (j == i || k == i) continue;
valid = true;
if (j == k)
{
makeLatin2(i, j);
break;
}
makeLatin(i, j, k);
break;
}
}
}
if (valid)
{
cout << "Case #" << t << ": POSSIBLE\n";
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++) cout << ans[i][j] << ' ';
cout << '\n';
}
}
else cout << "Case #" << t << ": IMPOSSIBLE\n";
}
}
|
'문제 풀이 > 그외' 카테고리의 다른 글
| Google Kick Start - Round F 2020 (0) | 2020.09.27 |
|---|---|
| Google Kick Start - Round E 2020 (2) | 2020.08.23 |
| SCPC 2020 Round 1 (2) | 2020.08.22 |
| Google Kick Start - Round D 2020 (0) | 2020.07.13 |
| Google Code Jam - Round 1A 2020 (2) | 2020.04.11 |



