

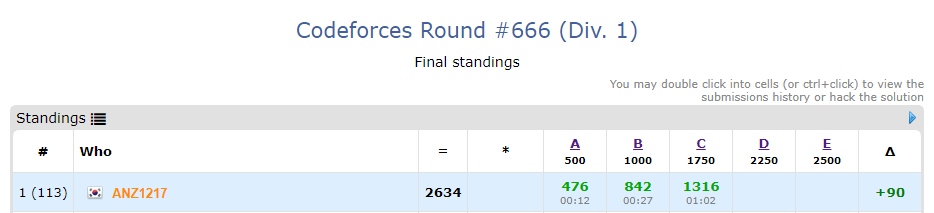
PS공부를 시작한지 1년하고도 4개월이 지났습니다.
이번 라운드로 레드를 달았습니다.
그동안 레드가 제 노력으로 갈 수 있는 최대라고 생각했습니다.
그래서 PS를 하면서 평생 목표중 하나이기도 했는데, 생각보다 빨리 달성해버려서 얼떨떨하면서도 너무 기쁩니다.
레드 찍으면 PS접는다고 주변에 말하고 다녔지만, 아무래도 그러진 못할것 같고 부계정이라도 하나 파서 계속 하려고 합니다.
물론 이제부터는 레이팅을 올려야 한다는 스트레스 없이 마음 편하게 공부할 수 있을 것 같습니다.
응원해주신 모든 분께 감사드립니다!
A - Juggling Letters
Problem - A - Codeforces
codeforces.com
\(n\)개의 문자열 배열 \(s\)가 주어진다.
한번의 연산으로, 문자열 \(s_i\)에서 문자 하나를 삭제한 다음, \(s_j\)의 임의의 위치에 추가할 수 있다.
연산을 원하는 만큼 할 수 있을 때, 모든 문자열이 같도록 할 수 있는지 여부를 알아내야 한다.
각 알파벳의 개수를 셌을 때, 개수가 \(n\)으로 나눠떨어지지 않는 알파벳이 존재한다면 불가능하다.
그렇지 않다면 가능하다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
ll gcd(ll a, ll b) { for (; b; a %= b, swap(a, b)); return a; }
int n;
int cnt[26];
int main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
int t; cin >> t;
while (t--)
{
memset(cnt, 0, sizeof cnt);
cin >> n;
for (int i = 0; i < n; i++)
{
string s; cin >> s;
for (char c : s) cnt[c - 'a']++;
}
bool ans = true;
for (int i = 0; i < 26; i++)
{
if (cnt[i] % n) ans = false;
}
if (ans) cout << "YES\n";
else cout << "NO\n";
}
}
|
B - Power Sequence
Problem - B - Codeforces
codeforces.com
어떤 \(n\)길이의 배열 \(a\)가 임의의 양수 \(c\)에 대해, \(a_i = c^i\)를 만족한다면, 이 배열을 power sequence라고 한다. (0-index)
\(n\) 길이의 배열 \(a\)가 주어진다.
이 배열에 다음과 같은 연산을 할 수 있다.
1. 배열 원소들의 위치를 바꾼다. (비용 0)
2. 임의의 원소 하나를 골라 1을 빼거나, 1을 더한다. (비용 1)
\(a\)를 power sequence로 만들기 위해 필요한 최소 비용을 알아내야 한다.
우선 배열을 정렬하자.
\(c\)가 \(\lfloor \sqrt[{n-1}]{a_{n-1}} \rfloor\) 보다 작다면, 답이 될 수 없다.
따라서 \(c\)를 \(\lfloor \sqrt[{n-1}]{a_{n-1}} \rfloor\)부터 시작해 1씩 늘려나가면서 답을 찾으면 된다.
\(c^x\)는 \(c\)가 증가함에 따라 매우 빠르게 증가하는 함수이기 때문에, 몇 번안에 답이 나오게 된다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
|
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
ll gcd(ll a, ll b) { for (; b; a %= b, swap(a, b)); return a; }
ll n;
ll a[100001];
int main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n;
for (int i = 0; i < n; i++) cin >> a[i];
sort(a, a + n);
ll st = pow(a[n - 1], 1.0 / (n - 1));
ll ans = numeric_limits<ll>::max();
bool flag = true;
for (ll k = 0; flag; k++)
{
ll res = 0;
ll mul = 1;
for (int i = 0; i < n; i++)
{
res += llabs(mul - a[i]);
if (res > ans)
{
flag = false;
break;
}
mul *= st + k;
}
if(flag) ans = min(ans, res);
}
cout << ans;
}
|
A - Multiples of Length
Problem - A - Codeforces
codeforces.com
\(n\)길이의 배열 \(a\)가 주어진다.
이 배열에 다음과 같은 연산을 정확히 3번 수행해 모든 원소를 0으로 만들어야 한다.
- 배열의 어떤 구간을 골라, 이 구간의 원소들에 \(len\)의 배수를 더한다. (\(len\)은 구간의 길이)
먼저 배열의 맨 첫번째 원소를 0으로 바꾼다.
배열의 2번째부터 \(n\)번째까지 구간에 고른 후 원소 \(a_i\)에 대해, \(a_i \times (n-1)\)을 더하면, 이 원소들은 모두 \(n\)으로 나누어 떨어지게 된다.
마지막에 배열 전체를 골라 전부 0으로 바꿔주면 된다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
|
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
ll gcd(ll a, ll b) { for (; b; a %= b, swap(a, b)); return a; }
ll n;
ll a[100001];
int main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n;
for (int i = 0; i < n; i++) cin >> a[i];
cout << "1 1\n";
cout << -a[0] << '\n';
a[0] = 0;
if (n >= 2)
{
cout << "2 " << n << '\n';
for (int i = 1; i < n; i++)
{
cout << (n - 1) * a[i] << ' ';
a[i] += (n - 1) * a[i];
}
cout << '\n';
cout << "1 " << n << '\n';
for (int i = 0; i < n; i++)
{
cout << -a[i] << ' ';
}
}
else
{
cout << "1 1\n";
cout << "0\n";
cout << "1 1\n";
cout << "0\n";
}
}
|
B - Stoned Game
Problem - B - Codeforces
codeforces.com
\(n\)더미의 돌이 있다. 각 더미에는 \(a_i\)개의 돌이 있다.
두 사람이 게임을 한다. 각 차례에 플레이어는 비어있지 않은 더미를 하나 골라, 돌을 하나 제거할 수 있다.
단, 그 전차례에 골라진 더미는 고를 수 없다.
본인 차례에 돌을 제거할 수 없으면 패배한다.
돌 더미들의 상태가 주어지면, 선공과 후공 중 누가 일지 알아내야 한다.
만약 어떤 돌 더미에 있는 돌의 개수가 전체 돌의 개수의 절반보다 많다면, 선공이 이 돌 더미에서만 돌을 제거하는 것을 반복함으로써 무조건 승리할 수 있다.
그런 돌 더미가 없다면, 승패는 총 돌의 개수로만 결정되어짐을 관찰로써 알 수 있다.
총 돌의 개수가 홀수라면 선공, 짝수라면 후공이 승리한다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
|
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
ll gcd(ll a, ll b) { for (; b; a %= b, swap(a, b)); return a; }
int n;
int a[101];
int main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
int t; cin >> t;
while (t--)
{
cin >> n;
int sum = 0;
for (int i = 0; i < n; i++)
{
cin >> a[i];
sum += a[i];
}
if (n == 1)
{
cout << "T\n";
continue;
}
bool flag = false;
for (int i = 0; i < n; i++)
{
if (a[i] > sum - a[i]) flag = true;
}
if (flag)
{
cout << "T\n";
continue;
}
if (sum % 2 == 0) cout << "HL\n";
else cout << "T\n";
}
}
|
C - Monster Invaders
Problem - C - Codeforces
codeforces.com
\(n\)개의 레벨로 이루어진 게임이 있다.
각 레벨은 \(a_i\)마리의 일반 몬스터 (1 hp), 1마리의 보스 몬스터 (2 hp)로 이루어져 있다.
이 몬스터들을 처치하기 위해 다음과 같은 무기로 공격을 할 수 있다.
권총 : 임의의 몬스터에 1의 대미지를 준다. 공격에 \(r_1\)의 시간이 걸린다.
레이저 건 : 모든 몬스터에 1의 대미지를 준다. 공격에 \(r_2\)의 시간이 걸린다.
AWP : 임의의 몬스터를 즉시 죽인다. 공격에 \(r_3\)의 시간이 걸린다.
어떤 레벨에서 일반 몬스터를 모두 죽이기 전까지는, 보스 몬스터에 권총이나 AWP를 사용할 수 없다.
또 보스 몬스터를 공격했음에도 불구하고 보스 몬스터가 죽지 않았을 경우, 무조건 인접한 레벨로 이동해야 한다.
인접한 레벨로 이동하는데는 \(d\)의 시간이 걸린다.
처음에 1번 레벨에서 시작할 때, 모든 몬스터를 처치하는데 걸리는 최소 시간을 알아내야 한다.
각 레벨을 완료하기 위해 다음과 같은 3가지 방법중 하나를 사용할 수 있다.
1. 모든 일반 몬스터를 권총 또는 AWP로 죽인다음, 보스 몬스터를 AWP로 처치하고 다음 레벨로 이동한다.
2. 모든 일반 몬스터를 권총 또는 AWP로 죽인다음, 보스 몬스터를 권총으로 1번 공격한다음, 다른 레벨을 갔다 와서 보스 몬스터를 임의의 무기로 다시 공격한다.
3. 레이저 건으로 모든 몬스터를 공격한다음, 다른 레벨을 갔다 와서 보스 몬스터를 임의의 무기로 다시 공격한다.
그러면 다음과 같이 DP를 정의할 수 있다.
\(DP(0, i)\) : 전 단계의 보스 몬스터를 이미 죽였을 때, 현재 단계부터 시작해 모든 몬스터를 죽이는데 필요한 최소 시간
\(DP(1, i)\) : 전 단계의 보스 몬스터의 체력이 1 남았을 때, 현재 단계부터 시작해 모든 몬스터를 죽이는데 필요한 최소 시간
답은 \(DP(0, 1)\)이다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
|
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
ll gcd(ll a, ll b) { for (; b; a %= b, swap(a, b)); return a; }
const ll INF = numeric_limits<ll>::max();
ll n, r1, r2, r3, d;
ll a[1000001];
ll dp[2][1000001];
ll solve(int t, int idx)
{
ll& ret = dp[t][idx];
if (idx == n)
{
if (t == 0) return ret = 0;
return ret = d + d + min(r1, min(r2, r3));
}
if (ret != -1) return ret;
ll t1 = min(r1, r3) * a[idx] + r3;
if (t)
{
t1 += d + min(r1, min(r2, r3));
if (idx != n - 1) t1 += d;
}
t1 += solve(0, idx + 1);
ll t2 = min(r1, r3) * a[idx] + min(r1, r2);
if (t)
{
t2 += d + min(r1, min(r2, r3));
t2 += d + min(r1, min(r2, r3));
t2 += solve(0, idx + 1);
}
else
{
t2 += solve(1, idx + 1);
}
ll t3 = r2;
if (t)
{
t3 += d + min(r1, min(r2, r3));
t3 += d + min(r1, min(r2, r3));
t3 += solve(0, idx + 1);
}
else
{
t3 += solve(1, idx + 1);
}
return ret = min(t1, min(t2, t3));
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> r1 >> r2 >> r3 >> d;
for (int i = 0; i < n; i++) cin >> a[i];
memset(dp, -1, sizeof dp);
ll ans = solve(0, 0) + d * (n - 1);
cout << ans;
}
|
D - Rainbow Rectangles
Problem - D - Codeforces
codeforces.com
추가 예정
E - Distance Matching
Problem - E - Codeforces
codeforces.com
추가 예정
'문제 풀이 > Codeforces' 카테고리의 다른 글
| Codeforces Round #669 (Div. 2) (0) | 2020.09.09 |
|---|---|
| Codeforces Round #668 (Div. 1, Div. 2) (0) | 2020.09.07 |
| Codeforces Global Round 10 (0) | 2020.08.18 |
| Educational Codeforces Round 93 (1) | 2020.08.15 |
| Codeforces Round #663 (Div. 2) (0) | 2020.08.10 |
