
A - C+=
Problem - A - Codeforces
codeforces.com
정수 \(a, b\)가 주어진다.
이 정수들에 다음의 두 가지 연산을 할 수 있다.
1. \(a\) += \(b\)
2. \(b\) += \(a\)
이 때, \(a\)나 \(b\)가 \(n\)보다 크도록 만들기 위한 연산 횟수의 최소값을 구해야 한다.
관찰로 더 작은 수의 크기를 늘리는게 무조건 이득이라는 사실을 알 수 있다.
그러면 전체적인 수의 크기가 지수함수의 형태로 증가하므로, 단순 시뮬레이션으로도 충분히 시간안에 돌아가게 된다.
실제로 최악인 \(a=b=1, n=10^9\)를 넣어도 43번의 연산안에 완료됨으로 확인할 수 있다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
ll gcd(ll a, ll b) { for (; b; a %= b, swap(a, b)); return a; }
int main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
int T; cin >> T;
while (T--)
{
ll a, b, n; cin >> a >> b >> n;
int ans = 0;
while (a <= n && b <= n)
{
if (a > b) swap(a, b);
a += b;
ans++;
}
cout << ans << '\n';
}
}
|
B - Codeforces Subsequences
Problem - B - Codeforces
codeforces.com
정수 \(k\)가 주어진다.
"codeforces" 라는 문자열이 부분 문자열로 \(k\)번 이상 등장하는 가장 짧은 문자열을 출력해야 한다.
문자 'c'가 \(cnt_1\)개, 'o'가 \(cnt_2\)개, 'd'가 \(cnt_3\)개... 's'가 \(cnt_{10}\)개씩 연속으로 이루어진 문자열을 생각해보자.
여기에서 부분 문자열이 "codeforces"인 부분 문자열의 개수는 \(cnt_1 \times cnt_2 \times \cdots \times cnt_{10}\)이다.
여기에서 한 글자를 더 추가해야 한다면, \(cnt_i\)가 가장 작은 값에 1을 더하는 것이 가장 이득임을 알 수 있다.
역시 시뮬레이션으로 곱이 \(k\)보다 커질때까지 반복하면 된다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
ll gcd(ll a, ll b) { for (; b; a %= b, swap(a, b)); return a; }
string cf = "codeforces";
ll cnt[10];
int main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
for (int i = 0; i < 10; i++) cnt[i] = 1;
ll k; cin >> k;
if (k == 1)
{
cout << cf;
return 0;
}
while (true)
{
for (int j = 0; j < 10; j++)
{
cnt[j]++;
ll res = 1;
for (int i = 0; i < 10; i++) res *= cnt[i];
if (res >= k)
{
for (int l = 0; l < 10; l++)
{
for (int m = 0; m < cnt[l]; m++) cout << cf[l];
}
return 0;
}
}
}
}
|
C - Even Picture
Problem - C - Codeforces
codeforces.com
격자에 다음 조건을 만족하는 색칠을 하려고 한다.
1. 색칠한 칸은 모두 이어져 있어야 한다.
2. 모든 칸은 짝수 개의 다른 색칠된 칸과 인접해 있어야 한다.
3. 정확히 \(n\)개의 칸은 4개의 색칠된 칸과 인접해 있어야 한다.
위의 조건을 만족하도록 색칠된 칸들의 좌표를 출력하면 된다.
다음과 같이 색칠하면 위의 조건을 만족한다.
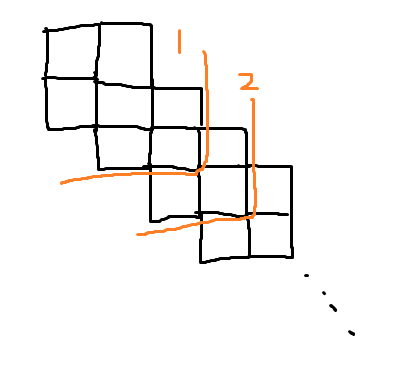
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
ll gcd(ll a, ll b) { for (; b; a %= b, swap(a, b)); return a; }
int main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
int n; cin >> n;
cout << 4 + 3 * n << '\n';
cout << "0 0\n";
cout << "0 1\n";
cout << "1 0\n";
cout << "1 1\n";
for (int i = 0; i < n; i++)
{
cout << i + 1 << ' ' << i + 2 << '\n';
cout << i + 2 << ' ' << i + 1 << '\n';
cout << i + 2 << ' ' << i + 2 << '\n';
}
}
|
D - AND, OR and square sum
Problem - D - Codeforces
codeforces.com
\(n\)개의 원소로 이루어진 배열 \(a\)가 주어진다.
이 배열에서 다음과 같은 연산을 할 수 있다.
1. 서로 다른 두 인덱스 \(i,j\)를 고른다.
2. \(x = a[i], y = a[j]\)라고 했을 때, \(a[i]\)를 \(x \text{ AND } y\)로, \(a[j]\)를 \(x \text{ OR } y\)로 바꾼다.
연산을 마치고 나서 배열의 모든 원소의 제곱의 합이 최대가 되도록 했을 때, 그 값을 알아내야 한다.
어떤 두 수 \(a, b\)에 위의 연산을 했을 때, 두 수 중 하나에만 있는 비트가 한 쪽으로 몰리게 된다.
따라서 연산 전후 배열의 원소의 합은 일정하므로, 제곱의 합이 최대가 되게 하려면 최대한 비트를 하나의 원소에 몰아서 단일 원소가 커지게 하는 것이 이득이라는 것을 알 수 있다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
|
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
ll gcd(ll a, ll b) { for (; b; a %= b, swap(a, b)); return a; }
int n;
ll cnt[20];
int main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n;
for (int i = 0; i < n; i++)
{
ll a; cin >> a;
for (int j = 0; j < 20; j++)
{
if (a & (1ll << j)) cnt[j]++;
}
}
ll ans = 0;
while (true)
{
ll mx = 987654321;
ll res = 0;
for (int i = 0; i < 20; i++)
{
if (cnt[i] == 0) continue;
res |= (1ll << i);
mx = min(mx, cnt[i]);
}
ans += mx * res * res;
for (int i = 0; i < 20; i++)
{
if (cnt[i] == 0) continue;
cnt[i] -= mx;
}
if (res == 0) break;
}
cout << ans;
}
|
E - Ski Accidents
Problem - E - Codeforces
codeforces.com
\(n\)개의 정점과 \(m\)개의 간선으로 이루어진 DAG가 있다.
각 정점은 최대 2개의 진출 간선을 가진다.
이 그래프에서 최대 \(\frac 74 n\)개의 정점을 없애서, 그래프에 길이가 2 이상인 경로가 존재하지 않게 하려고 한다.
정점을 없애면 여기에 연결된 진출/진입 간선이 모두 없어진다.
없애야 하는 정점을 모두 출력하면 된다.
정점을 위상 정렬한 다음 차례대로 살펴보자.
이 정점을 포함했을 때 길이 2 이상인 경로가 존재하게 된다면 삭제하는 식으로 정하면 된다.
자세한 증명은 에디토리얼을 참고하자..
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
|
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
ll gcd(ll a, ll b) { for (; b; a %= b, swap(a, b)); return a; }
int n, m;
vector <int> graph[200001];
int in[200001];
int mx[200001];
int res[200001];
int main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
int T; cin >> T;
while (T--)
{
cin >> n >> m;
for (int i = 1; i <= n; i++)
{
graph[i].clear();
in[i] = 0;
mx[i] = 0;
}
for (int i = 0; i < m; i++)
{
int u, v; cin >> u >> v;
graph[u].push_back(v);
in[v]++;
}
queue <int> q;
for (int i = 1; i <= n; i++)
{
if (in[i] == 0) q.push(i);
}
while (!q.empty())
{
int v = q.front(); q.pop();
if (mx[v] == 2) res[v] = 0;
else res[v] = mx[v] + 1;
for (int nv : graph[v])
{
mx[nv] = max(mx[nv], res[v]);
if (--in[nv] == 0) q.push(nv);
}
}
vector <int> ans;
for (int i = 1; i <= n; i++)
if (res[i] == 0) ans.push_back(i);
cout << ans.size() << '\n';
for (int v : ans) cout << v << ' ';
cout << '\n';
}
}
|
F - Lamps on a Circle
Problem - F - Codeforces
codeforces.com
컴퓨터와 게임을 하려고 한다.
\(n\)개의 램프가 원형으로 늘어서 있다.
내 차례에 게임을 끝내거나, 임의의 \(k\)개의 램프를 선택해 꺼져 있는 램프를 켤 수 있다.
게임이 끝나지 않았다면, 다음 차례에 컴퓨터는 연속된 \(k\)개의 램프를 선택해 켜져 있는 램프를 끈다.
많아도 \(10^4\)번의 차례안에 게임을 끝내야 하고,
게임이 끝나고 나서 켜져 있는 램프의 수를 최대화 해야 한다.
현재 턴에 내가 \(k\)개를 켠 다음, 다음 턴에서 \(k\)개가 제거되지 않도록 하려면, 램프를 켠 결과 연속된 \(k\)개가 켜져 있는 상태가 아니어야 한다.
연속된 \(k\)개의 랜턴이 켜져있지 않으려면 최소 \(\lfloor \frac nk \rfloor\)개의 랜턴은 켜져 있을 수 없음을 뜻하므로,
내 턴이 끝나고 나면 최대 \(n - \lfloor \frac nk \rfloor\)개의 랜턴이 켜져 있을 수 있고, 컴퓨터의 턴이 끝나면
최대 \(n - \lfloor \frac nk \rfloor - (k-1)\)개의 랜턴이 켜져 있을 수 있다.
\(2 \le i \le n\)에 대해 이 값을 계산해 최대값일 때의 \(k\)를 알아낸 다음,
내 차례 때 켜지 않을 램프를 정한 뒤 그 램프들을 제외한 \(k\)개를 켜는 것을 반복하면 된다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
|
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
ll gcd(ll a, ll b) { for (; b; a %= b, swap(a, b)); return a; }
int n;
int tmp[1001];
int ocp[1001];
int main()
{
cin >> n;
if (n < 4)
{
cout << 0 << endl;
return 0;
}
int sz = 0;
int ans = 0;
for (int i = 2; i <= n; i++)
{
int res = n - ((n - 1) / i + 1) - (i - 1);
if (res > ans)
{
ans = res;
sz = i;
}
}
for (int i = 0; i * sz < n; i++)
{
tmp[i * sz + 1] = 1;
}
while (true)
{
vector <int> query;
for (int i = 1; i <= n; i++)
{
if (tmp[i] || ocp[i]) continue;
ocp[i] = 1;
query.push_back(i);
if (query.size() == sz) break;
}
cout << query.size();
for (int i : query) cout << ' ' << i;
cout << endl;
int res; cin >> res;
for (int i = 0; i < sz; i++)
{
ocp[(res - 1 + i) % n + 1] = 0;
}
int cnt = 0;
for (int i = 1; i <= n; i++)
{
if (ocp[i]) cnt++;
}
if (cnt >= ans) break;
}
cout << 0 << endl;
}
|
G - Shifting Dominoes
Problem - G - Codeforces
codeforces.com
추가 예정
H - Breadboard Capacity (hard version)
Problem - H2 - Codeforces
codeforces.com
추가 예정
'문제 풀이 > Codeforces' 카테고리의 다른 글
| Codeforces Round #652 (Div. 2) (0) | 2020.06.24 |
|---|---|
| Codeforces Round #651 (Div. 2) (0) | 2020.06.21 |
| Codeforces Round #650 (Div. 3) (0) | 2020.06.17 |
| Codeforces Round #648 (Div. 2) (0) | 2020.06.08 |
| Codeforces Round #647 (Div. 1, Div.2) - Thanks, Algo Muse! (0) | 2020.06.05 |

