분할 정복은 큰 문제를 분할하여 단순한 부분 문제로 만든 다음, 각 부분 문제의 답으로부터 전체 문제의 답을 이끌어내는 방식의 알고리즘입니다.
역시 분할 정복 자체만으로 풀 수 있는 문제는 그렇게 많지 않지만, 분할 정복은 다른 많은 알고리즘들의 기본 아이디어가 됩니다.
분할 정복으로 풀 수 있는 문제들의 예를 몇가지 살펴보도록 합시다.
https://www.acmicpc.net/problem/2630
2630번: 색종이 만들기
첫째 줄에는 전체 종이의 한 변의 길이 N이 주어져 있다. N은 2, 4, 8, 16, 32, 64, 128 중 하나이다. 색종이의 각 가로줄의 정사각형칸들의 색이 윗줄부터 차례로 둘째 줄부터 마지막 줄까지 주어진다. 하얀색으로 칠해진 칸은 0, 파란색으로 칠해진 칸은 1로 주어지며, 각 숫자 사이에는 빈칸이 하나씩 있다.
www.acmicpc.net
\(N \times N\)크기의 색종이가 있습니다. 이 색종이의 각 칸은 하얀색 또는 파란색으로 칠해져 있습니다.
이 색종이를 자르려고 하는데, 색종이를 자르는 규칙은 다음과 같습니다.
이 종이가 모두 같은 색으로 칠해져 있지 않으면, 같은 크기의 \(\frac n2 \times \frac n2\)크기의 색종이 4개로 자릅니다.
나누어진 종이 각각에 대해서도, 모두 같은 색으로 칠해져 있지 않으면 자르는 것을 반복합니다.
이 방식으로 더 이상 색종이를 자를 수 없을 때까지 반복했을 때, 나오는 하얀색 색종이의 수와 파란색 색종이의 개수를 구해야 합니다.
가장 기본적인 분할정복 문제입니다.
현재 보고 있는 정사각형이 모두 한 색깔로 칠해져 있는지 확인한 다음, 칠해져 있으면 그 색의 개수에 1을 더하고, 그렇지 않으면 4등분해서 각각에 대해 답을 구한다음 합치면 됩니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
|
#include <iostream>
#include <algorithm>
using namespace std;
int n;
int paper[128][128];
pair <int, int> solve(int x, int y, int sz)
// 현재 좌상단의 좌표가 (x,y)이고 크기가 sz인 정사각형을 보고 있다.
{
int color = paper[x][y];
bool isSame = true;
for (int i = x; i < x + sz; i++) for (int j = y; j < y + sz; j++)
{
if (paper[i][j] != color)
isSame = false;
// 현재 보고 있는 정사각형이 모두 같은 색으로 칠해져 있는지 확인한다.
}
if (isSame)
{
// 모두 같으면 답을 반환한다
if (color == 0) return { 1,0 };
else return { 0,1 };
}
pair <int, int> res = { 0,0 };
for (int i = 0; i < 2; i++) for (int j = 0; j < 2; j++)
{
pair <int, int> tmp = solve(x + i * sz / 2, y + j * sz / 2, sz / 2);
res.first += tmp.first;
res.second += tmp.second;
// 그렇지 않다면 4등분해서 각각 답을 계산한 후 합쳐준다.
}
return res;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n;
for (int i = 0; i < n; i++) for (int j = 0; j < n; j++)
cin >> paper[i][j];
pair <int, int> ans = solve(0, 0, n);
cout << ans.first << '\n' << ans.second;
}
|
https://www.acmicpc.net/problem/6549
6549번: 히스토그램에서 가장 큰 직사각형
문제 히스토그램은 직사각형 여러 개가 아래쪽으로 정렬되어 있는 도형이다. 각 직사각형은 같은 너비를 가지고 있지만, 높이는 서로 다를 수도 있다. 예를 들어, 왼쪽 그림은 높이가 2, 1, 4, 5, 1, 3, 3이고 너비가 1인 직사각형으로 이루어진 히스토그램이다. 히스토그램에서 가장 넓이가 큰 직사각형을 구하는 프로그램을 작성하시오. 입력 입력은 테스트 케이스 여러 개로 이루어져 있다. 각 테스트 케이스는 한 줄로 이루어져 있고, 직사각형의 수 n이
www.acmicpc.net
\(n\)개의 직사각형으로 이루어진 히스토그램이 주어집니다.
이 히스토그램안에 포함되면서 축에 평행한 직사각형 중 가장 넓이가 큰 직사각형의 넓이를 구해야 합니다.
주어지는 히스토그램을 반으로 나눠봅시다.

그럼 가장 큰 직사각형은 다음 3가지 중에 1가지에 해당됩니다.
1. 직사각형이 왼쪽 절반 내에 존재한다.
2. 직사각형이 오른쪽 절반 내에 존재한다.
3. 직사각형이 왼쪽과 오른쪽 모두에 걸쳐있다.
1번과 2번은 재귀로 넘겨주면 되니까 넘어가고, 3번에 해당되는 직사각형의 넓이를 구해봅시다.

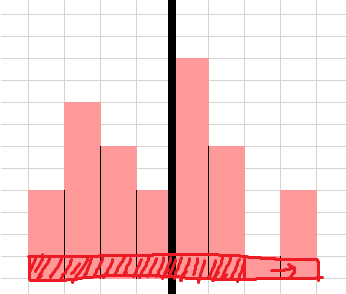
두 영역에 모두 걸치면서 가장 넓은 직사각형은 당연히 절반을 나눈 선에 맞닿아있는 두 직사각형을 포함합니다.
따라서 너비가 2이고, 높이가 두 직사각형 중 낮은 값인 직사각형을 만들 수 있습니다.
이 직사각형을 기준으로, 왼쪽 또는 오른쪽으로 한칸씩 너비를 넓혀가면서 새로운 직사각형을 만들어봅시다.
둘 중 어느 방향으로 먼저 넓히는 것이 유리할까요?
잘 생각해보면, 두 방향에 있는 직사각형 중 높이가 더 높은쪽으로 넓혀나가는게 이득임을 알 수 있습니다.
양쪽의 직사각형의 높이가 현재 직사각형의 높이보다 높거나 같다면 상관 없지만, 현재 직사각형의 높이보다 낮다면 높이가 낮아짐에 따라 전체 넓이가 작아질 수 있기 때문입니다.
따라서 위의 직사각형은
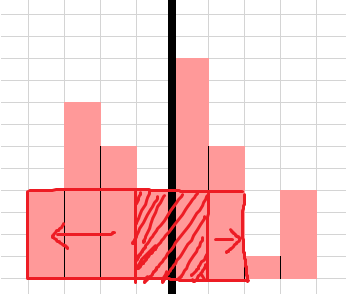
높이가 4칸인 상태로 최대 너비 6칸까지 넓혀나갈 수 있고,
그 후 오른쪽으로 넓혀나가면서 높이가 1이 되며, 이 상태로 최대 너비 8칸까지 넓혀나갈 수 있습니다.
따라서 두 영역을 모두 걸치는 직사각형의 최대 넓이는 높이 4, 너비 6일때의 24임을 알 수 있습니다.
이런식으로 계산 한 다음, 1번과 2번을 재귀로 계산한 값을 얻어온 다음, 세 값중 최대값이 답이 됩니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
|
#include <iostream>
#include <algorithm>
using namespace std;
int n;
long long h[100001];
long long solve(int l, int r) // l번째 부터 r번째 인덱스에 있는 직사각형들을 보고 있다.
{
int sz = r - l + 1;
if (sz == 1) return h[l]; // 크기가 1이라면 그 직사각형의 크기를 반환한다.
int mid = (l + r) / 2;
int lptr = mid, rptr = mid + 1;
long long height = min(h[mid], h[mid + 1]);
long long ans = height * 2;
while (l < lptr || rptr < r)
{
long long left_height = -1;
long long right_height = -1;
if (lptr - 1 >= l) left_height = h[lptr - 1];
if (rptr + 1 <= r) right_height = h[rptr + 1];
if (left_height < right_height)
height = min(height, h[++rptr]);
else
height = min(height, h[--lptr]);
long long area = (rptr - lptr + 1) * height;
ans = max(ans, area);
// 양 방향 중에 더 높은 쪽으로 너비를 넓혀나가면서 최대 넓이를 갱신한다.
}
ans = max(ans, solve(l, mid));
ans = max(ans, solve(mid + 1, r));
// 왼쪽 절반과 오른쪽 절반에 속하는 경우를 재귀로 계산한다.
return ans;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
while (true)
{
cin >> n;
if (n == 0) break;
for (int i = 0; i < n; i++) cin >> h[i];
cout << solve(0, n - 1) << '\n';
}
}
|
이 풀이의 시간복잡도는 어떻게 될까요?
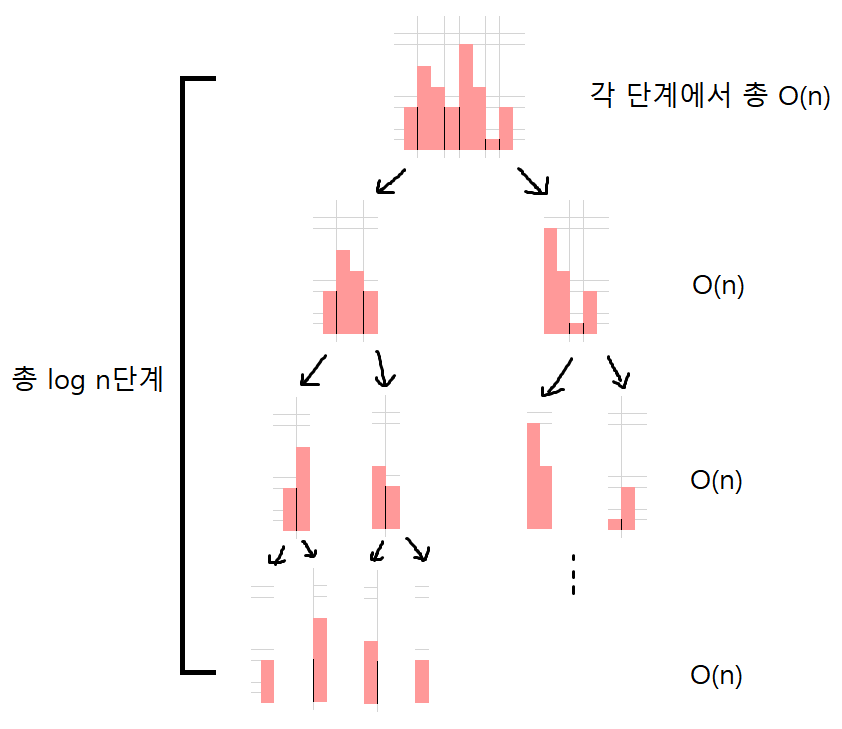
먼저 전체 히스토그램에 대해서, 3번에 해당하는 직사각형을 계산하는데 시간복잡도는 \(O(n)\)임을 쉽게 알 수 있습니다.
그 후 1번과 2번을 계산하는데, 각각 직사각형의 개수가 \(\frac n2\)개로 줄어들게 됩니다.
1번과 2번에 해당하는 직사각형을 계산할 때도 역시 현재 히스토그램을 반으로 나눈다음, 두 영역에 걸치는 직사각형을 구하는 작업을 해야 합니다.
이 때 각각에 해당하는 시간복잡도는 \(O(\frac n2)\)이므로, 역시 총 \(O(n)\)입니다.
결국 이 반으로 나눠지는 모든 단계 각각의 시간복잡도는 총 \(O(n)\)임을 알 수 있고,
이 단계의 수가 총 \(\log n\)개이므로, 총 시간복잡도는 \(O(n\log n)\)임을 알 수 있습니다.
https://www.acmicpc.net/problem/1920
1920번: 수 찾기
첫째 줄에 자연수 N(1≤N≤100,000)이 주어진다. 다음 줄에는 N개의 정수 A[1], A[2], …, A[N]이 주어진다. 다음 줄에는 M(1≤M≤100,000)이 주어진다. 다음 줄에는 M개의 수들이 주어지는데, 이 수들이 A안에 존재하는지 알아내면 된다. 모든 정수의 범위는 -231 보다 크거나 같고 231보다 작다.
www.acmicpc.net
수 \(N\)개가 주어집니다.
그 후 \(M\)개의 질의가 주어지는데, 질의로 주어진 수 \(X\)가 앞에서 주어진 수 \(N\)개안에 존재하는지 알아내야 합니다.
분할정복의 가장 대표적인 예중 하나인 이진 탐색 (Binary Search)에 대해 알아봅시다.
\(N\)개의 수를 정렬 한 다음, 한 가운데 있는 수를 기준으로 이 수가 \(X\)보다 큰지, 또는 작은지 확인해봅시다.
이 수가 \(X\)보다 크다면, \(X\)는 가운데보다는 왼쪽에 있을 것이고,
\(X\)보다 작다면, \(X\)는 가운데보다 오른쪽에 있을 겁니다.
한 번의 질의로 탐색하는 범위가 절반씩 줄어드므로, 각 질의에 대해 \(O(\log N)\)번의 탐색만으로 수의 존재여부를 확인할 수 있습니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
|
#include <iostream>
#include <algorithm>
using namespace std;
int n;
int a[100001];
int main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n;
for (int i = 0; i < n; i++) cin >> a[i];
sort(a, a + n); // 수들을 정렬한다.
int m; cin >> m;
while (m--)
{
int x; cin >> x;
int l = 0, r = n - 1; // 인덱스 l과 r사이에 수가 존재한다.
bool ans = false;
while (l <= r)
{
int mid = (l + r) / 2; // 중간값을 뽑아 x와 비교해본다.
if (a[mid] == x)
{
ans = true;
break;
// x를 찾았다.
}
else if (a[mid] > x)
{
r = mid - 1;
// 중간값이 x보다 크다면, x는 중간보다 왼쪽에 존재할 것이다.
}
else if (a[mid] < x)
{
l = mid + 1;
// 중간값이 x보다 작다면, x는 중간보다 오른쪽에 존재할 것이다.
}
}
if (ans) cout << "1\n";
else cout << "0\n";
}
}
|
또, C++에서는 이진탐색 함수를 제공하기 때문에 (binary_search, lower_bound, upper_bound), 다음과 같이 간단하게 풀 수도 있습니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
#include <iostream>
#include <algorithm>
using namespace std;
int n;
int a[100001];
int main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n;
for (int i = 0; i < n; i++) cin >> a[i];
sort(a, a + n); // 수들을 정렬한다.
int m; cin >> m;
while (m--)
{
int x; cin >> x;
if (binary_search(a, a + n, x)) cout << "1\n";
else cout << "0\n";
}
}
|
https://www.acmicpc.net/problem/1654
1654번: 랜선 자르기
첫째 줄에는 오영식이 이미 가지고 있는 랜선의 개수 K, 그리고 필요한 랜선의 개수 N이 입력된다. K는 1이상 10,000이하의 정수이고, N은 1이상 1,000,000이하의 정수이다. 그리고 항상 K ≦ N 이다. 그 후 K줄에 걸쳐 이미 가지고 있는 각 랜선의 길이가 센티미터 단위의 정수로 입력된다. 랜선의 길이는 231-1보다 작거나 같은 자연수이다.
www.acmicpc.net
이진 탐색의 응용문제입니다.
랜선의 길이의 범위가 매우 크므로, 모든 랜선의 길이를 하나하나 확인하면서 답을 찾는건 시간이 너무 오래 걸릴것임을 알 수 있습니다.
랜선의 길이의 후보는 \(1\)이상 \(2^{31}-1\)이하입니다.
이 후보에서 중간 값을 골라, 이 길이로 랜선을 만들었을 때 몇 개가 나오는지 확인해봅시다.
만약 원하는 랜선의 개수보다 더 적게 나온다면, 랜선의 길이가 더 짧아야 됩니다.
그렇지 않고 랜선의 개수보다 더 많이 나온다면, 랜선의 길이가 더 길어야 됩니다.
이 방법 역시 한번의 탐색으로 후보가 절반씩 줄어들게 되고, 한 번 탐색할 때 나오는 랜선의 수를 \(O(K)\)에 계산할 수 있으므로
총 시간복잡도 \(O(31 \cdot K)\)에 문제를 해결할 수 있게 됩니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
#include <iostream>
#include <algorithm>
using namespace std;
int k, n;
long long lan[10001];
int main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> k >> n;
for (int i = 0; i < k; i++) cin >> lan[i];
long long l = 1, r = 1ll << 31; // 가능한 랜선길이의 후보가 [l,r) 이다.
while (l + 1 < r)
{
long long mid = (l + r) / 2; // 랜선 길이가 mid일때 랜선의 길이를 센다.
long long cnt = 0;
for (int i = 0; i < k; i++)
{
cnt += lan[i] / mid;
}
if (cnt < n) r = mid; // 만약 원하는 개수보다 적다면, 랜선이 더 짧아야 한다.
else l = mid; // 원하는 개수보다 많거나 같다면, 랜선이 더 길어도 된다.
}
cout << l;
}
|
https://www.acmicpc.net/problem/1629
1629번: 곱셈
첫째 줄에 A, B, C가 빈 칸을 사이에 두고 순서대로 주어진다. A, B, C는 모두 2,147,483,647 이하의 자연수이다.
www.acmicpc.net
마지막으로 분할정복을 이용해 빠른 거듭제곱을 하는 법에 대해 알아봅시다.
단순히 \(A^B\)를 구하는 문제인데, \(B\)가 너무 커서 단순히 A를 B번 곱하는 식으로 풀면 시간안에 들어오지 못할 것 같습니다.
\(A^B\)를 다음과 같이 둘로 나눠서 계산해봅시다.
\(A^B = A^{B/2} \times A^{B/2}\)
앞의 \(A^{B/2}\)를 어떻게 계산했다고 합시다. 뒤의 \(A^{B/2}\)를 다시 계산할 필요가 있을까요?
아닙니다. 앞에서 계산했던 값을 거듭제곱하기만 하면 됩니다.
이 방식으로 \(A^B\)를 \(O(\log B)\)에 계산할 수 있게 됩니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
#include <iostream>
#include <algorithm>
using namespace std;
long long mpow(long long a, long long b, long long c) // a^b % c를 계산한다.
{
if (b == 0) return 1; // a^0은 1이다.
long long res = mpow(a, b / 2, c); // a^(b/2)를 계산한다.
res = res * res % c; // 결과를 거듭제곱한다.
if (b % 2 == 1) res = res * a % c; // b가 홀수면 a를 한번 더 곱해줘야 한다.
return res;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
long long a, b, c;
cin >> a >> b >> c;
cout << mpow(a, b, c);
}
|
제 그룹의 문제집에서 연습 문제들을 관리하고 있습니다.
문제집의 문제들을 보고 싶으시다면, 가입 신청을 해 주세요.
https://www.acmicpc.net/group/7712
ANZ1217
무슨 내용을 넣어야 좋을까요?
www.acmicpc.net
'알고리즘 > 시작하기' 카테고리의 다른 글
| PS를 공부하는 뉴비들을 위한 안내서 (15) | 2022.01.03 |
|---|---|
| 탐욕법 (Greedy) (0) | 2020.04.16 |
| 완전 탐색 (Brute Force) (0) | 2020.04.14 |
| 알고리즘의 시간복잡도 (0) | 2020.04.10 |
| Problem Solving 시작하기 (0) | 2020.04.10 |

