CCW

세 점 \(A, B, C\)가 있습니다.

이 점들을 이용해 2개의 벡터 \(\overrightarrow{AB}, \overrightarrow{BC}\)를 만듭시다.

 

이 두 벡터의 외적값을 이용해 세 점에 대한 방향성을 알 수 있습니다.

 

1. \(\overrightarrow{AB} \times \overrightarrow{BC} > 0\)

A - B - C는 좌회전합니다.

\(\overrightarrow{AB}\)에 비교했을 때, \(\overrightarrow{BC}\)의 방향은 반시계 방향입니다. (CCW)

 

2. \(\overrightarrow{AB} \times \overrightarrow{BC} < 0\)

A - B - C는 우회전합니다.

\(\overrightarrow{AB}\)에 비교했을 때, \(\overrightarrow{BC}\)의 방향은 시계 방향입니다. (CW)

 

3. \(\overrightarrow{AB} \times \overrightarrow{BC} = 0\)

A - B - C는 일직선 상에 위치합니다.

\(\overrightarrow{AB}\)와 \(\overrightarrow{BC}\)의 방향은 같습니다.

 

www.acmicpc.net/problem/11758

11758번: CCW

#include <bits/stdc++.h>
using namespace std;
 
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
 
ll gcd(ll a, ll b) { for (; b; a %= b, swap(a, b)); return a; }
 
int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0), cout.tie(0);
 
    int x1, y1, x2, y2, x3, y3;
    cin >> x1 >> y1 >> x2 >> y2 >> x3 >> y3;
 
    int v1_x = x2 - x1;
    int v1_y = y2 - y1;
 
    int v2_x = x3 - x2;
    int v2_y = y3 - y2;
 
    int ccw = v1_x * v2_y - v1_y * v2_x;
    if (ccw > 0) cout << 1;
    else if (ccw < 0) cout << -1;
    else cout << 0;
}

---

CCW를 이용하면, 일반적으로 실수 연산이 필요한 다양한 기하 문제들을 정수 연산만으로도 풀 수 있게 됩니다.

 

www.acmicpc.net/problem/17387

17387번: 선분 교차 2

선분 교차 판별을 해 봅시다.

 

두 선분에 대한 방정식을 세워 교차점을 계산하는 방법을 쓸 수도 있겠지만, CCW를 이용해 더 간단하게 풀 수 있습니다.

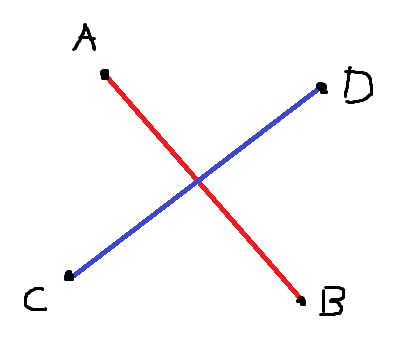
선분 \(\overline {AB}\)와 선분 \(\overline {CD}\)가 교차하려면 다음 2가지를 만족해야 합니다.

 

1. A-B-C의 방향과 A-B-D의 방향이 다르다.

2. C-D-A의 방향과 C-D-B의 방향이 다르다.

 

 

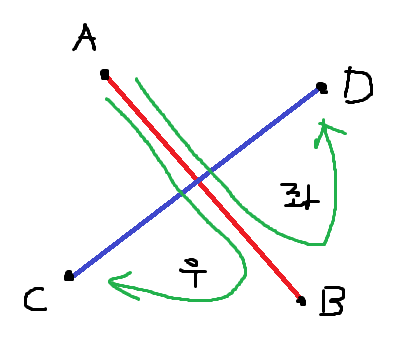
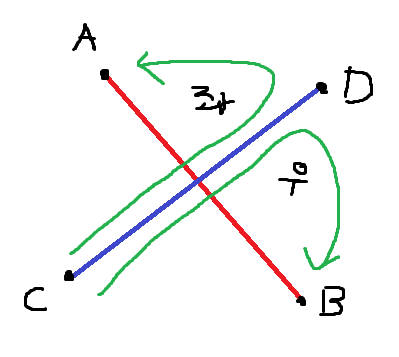
한 가지 예외가 존재하는데, 네 점이 모두 일직선 상에 있을 때는 모든 CCW값이 0으로 나오게 됩니다.

이 때는 점의 좌표값의 대소를 비교하여 교차를 판별할 수 있습니다.

 

 

#include <bits/stdc++.h>
using namespace std;
 
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
 
ll gcd(ll a, ll b) { for (; b; a %= b, swap(a, b)); return a; }
 
pll p2v(pll a, pll b) // 두 점 A,B가 주어지면 벡터 AB를 반환
{
    return { b.first - a.first, b.second - a.second };
}
 
ll ccw(pll v1, pll v2) // 벡터 v1, v2의 CCW
{
    ll res = v1.first * v2.second - v1.second * v2.first;
 
    if (res > 0) return 1;
    else if (res < 0) return -1;
    else return 0;
}
 
int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0), cout.tie(0);
 
    pll a, b, c, d;
    cin >> a.first >> a.second;
    cin >> b.first >> b.second;
    cin >> c.first >> c.second;
    cin >> d.first >> d.second;
 
    bool areIntersect = true;
 
    pll vec_ab = p2v(a, b);
    pll vec_bc = p2v(b, c);
    pll vec_bd = p2v(b, d);
 
    pll vec_cd = p2v(c, d);
    pll vec_da = p2v(d, a);
    pll vec_db = p2v(d, b);
 
    ll r1 = ccw(vec_ab, vec_bc);
    ll r2 = ccw(vec_ab, vec_bd);
 
    ll r3 = ccw(vec_cd, vec_da);
    ll r4 = ccw(vec_cd, vec_db);
 
    if (r1 == r2)
    {
        if (r1) areIntersect = false; // abc, abd의 방향이 같다.
        else // 네 점이 일직선에 있다.
        {
            if (min(a.first, b.first) > max(c.first, d.first)
                || max(a.first, b.first) < min(c.first, d.first))
                areIntersect = false;
 
            if (min(a.second, b.second) > max(c.second, d.second)
                || max(a.second, b.second) < min(c.second, d.second))
                areIntersect = false;
        }
    }
 
    if (r3 && r3 == r4) areIntersect = false; // cda, cdb의 방향이 같다.
 
    if (areIntersect) cout << 1;
    else cout << 0;
}

---

제 그룹의 문제집에서 연습 문제들을 관리하고 있습니다.
문제집의 문제들을 보고 싶으시다면, 가입 신청을 해 주세요.

 

www.acmicpc.net/group/7712

ANZ1217