문자열 \(S\)가 주어졌을 때, 이 문자열의 모든 접미사(suffix)를 사전순으로 정렬해 봅시다.
가장 단순한 방법은 \(|S|\)개의 suffix를 만든다음, 직접 정렬하는 것입니다.
이 방법을 이용하면 \(O(n^2 \log n)\)의 시간복잡도로 Suffix Array를 만들 수 있습니다. (\(n = |S|\))
11656번: 접미사 배열
첫째 줄에 문자열 S가 주어진다. S는 알파벳 소문자로만 이루어져 있고, 길이는 1,000보다 작거나 같다.
www.acmicpc.net
물론 이는 문자열의 길이가 조금만 길어져도 쓸 수 없는 방법이므로, 다른 방법을 생각해 봅시다.
다음과 같은 문자열이 있습니다. (0-index)
\(S = \) "abracadabra"
먼저, 접미사 전체가 아니라 각 접미사의 첫 한 글자만을 이용해 Suffix Array를 만들면 다음과 같습니다.

왼쪽 표는 각 인덱스에서 시작하는 접미사에 대해, 앞 1글자만을 고려했을 때 해당하는 문자열과 우선순위입니다.
오른쪽 표는 이를 우선순위 순으로 정렬했을 때, 해당하는 문자열과 인덱스입니다.
또, 오른쪽 표에서 각 인덱스를 우선순위 순으로 정렬했을 때의 결과가 우리가 구하려는 Suffix Array입니다.
($는 문자열의 끝을 표시하기 위해 임의로 넣은 문자입니다. 실제로 구현할 때는 넣지 않아도 됩니다.)
이 결과를 이용하면 접미사의 첫 두 글자에 대한 Suffix Array도 만들 수 있습니다.
어떻게 할 수 있을까요?

우리는 현재 인덱스의 문자열과, 다음 인덱스의 문자열의 우선순위를 알고 있습니다.
이 두 우선순위로 이루어진 pair을 정렬함으로써 새로운 우선순위를 정해줄 수 있고, 이는 각 접미사의 첫 두 글자에 대한 우선순위가 됩니다.
같은 방법으로 첫 4글자의 Suffix Array도 만들 수 있습니다.
현재 인덱스 \(i\)의 문자열과, \(i+2\)의 문자열의 우선순위를 합치면 됩니다.

이를 8글자, 16글자까지 반복하면 우리가 원하는 Suffix Array를 구할 수 있게 됩니다.


이 작업의 시간복잡도에 대해 생각해 봅시다.
총 \(\log n\)단계의 작업으로 진행되고, 각 단계는 두 우선순위의 pair를 정렬하는 작업과, 그 결과에 맞게 우선순위와 Suffix Array를 재조정하는 작업으로 이루어 집니다.
이 중 가장 큰 우선순위를 가지는 것은 정렬로, \(O(n \log n)\)의 복잡도를 가집니다.
따라서, 총 시간복잡도는 \(O(n \log ^2n)\)입니다.
여기에서 pair에 대한 정렬을 Radix Sort등의 \(O(n)\) 정렬로 바꾸면, \(O(n \log n)\)의 시간복잡도로도 가능합니다.
Suffix Array를 이용해 문자열 검색을 \(O(|T| \log |S|)\)에 할 수 있습니다.
1786번: 찾기
첫째 줄에, T 중간에 P가 몇 번 나타나는지를 나타내는 음이 아닌 정수를 출력한다. 둘째 줄에는 P가 나타나는 위치를 차례대로 공백으로 구분해 출력한다. 예컨대, T의 i~i+m-1번 문자와 P의 1~m
www.acmicpc.net
\(S\)에서 \(T\)를 찾으려고 합니다.
우선 \(S\)에 대한 Suffix Array를 만듭시다.
어떤 \(S\)의 접미사의 접두사가 \(T\)와 일치한다면, 그 위치에 \(T\)가 있다는 뜻이 됩니다.
접미사가 정렬되어 있으므로, 이분 탐색으로 Suffix Array내에서의 lower bound와 upper bound를 찾음으로써 해결할 수 있습니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
|
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
ll gcd(ll a, ll b) { for (; b; a %= b, swap(a, b)); return a; }
string S, T;
int RA[2000001];
int SA[2000001];
int tmp[2000001];
int main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
getline(cin, S);
getline(cin, T);
for (int i = 0; i < S.size(); i++)
{
RA[i] = S[i]; // 초기 우선순위를 그 문자의 아스키코드로 설정한다.
SA[i] = i;
}
// O(nlog^2n) Suffix Array
for (int k = 1; k < S.size(); k *= 2)
{
auto cmp = [&k](int a, int b)
{
if (RA[a] != RA[b]) return RA[a] < RA[b];
int a2 = a + k < S.size() ? RA[a + k] : -1;
int b2 = b + k < S.size() ? RA[b + k] : -1;
return a2 < b2;
};
sort(SA, SA + S.size(), cmp);
// 두개의 우선순위 페어로 정렬
// 이 부분을 O(n)으로 바꾸면 O(nlogn)이다.
tmp[SA[0]] = 0;
for (int i = 1; i < S.size(); i++)
{
// 각 접미사의 첫 k문자의 우선순위가 같은지 여부 확인
if (!cmp(SA[i - 1], SA[i]) && !cmp(SA[i], SA[i - 1]))
tmp[SA[i]] = tmp[SA[i - 1]];
else
tmp[SA[i]] = tmp[SA[i - 1]] + 1;
}
for (int i = 0; i < S.size(); i++) RA[i] = tmp[i];
}
// 이분탐색으로 lower_bound, upper_bound를 찾는다
int l, r, lo, up;
l = -1, r = S.size();
while (l + 1 < r)
{
int m = (l + r) / 2;
if (T <= S.substr(SA[m], T.size())) r = m;
else l = m;
}
lo = r;
l = -1, r = S.size();
while (l + 1 < r)
{
int m = (l + r) / 2;
if (T < S.substr(SA[m], T.size())) r = m;
else l = m;
}
up = r;
vector <int> ans;
for (int i = lo; i < up; i++) ans.push_back(SA[i] + 1);
sort(ans.begin(), ans.end());
cout << ans.size() << '\n';
for (int v : ans) cout << v << ' ';
}
|
사실 Suffix Array만으로 풀 수 있는 문제는 거의 없습니다.
Suffix Array에 대한 LCP(Longest Common Prefix, 최장 공통 접두사)를 구하면 해결할 수 있는 문제가 많아지게 됩니다.
LCP 배열은 Suffix Array에서 \(i\)번째 접미사와 \(i-1\)접미사의 LCP를 구한 배열입니다.
예를 들어 \(S = \) "abracadabra" 일때, LCP 배열은 다음과 같습니다.
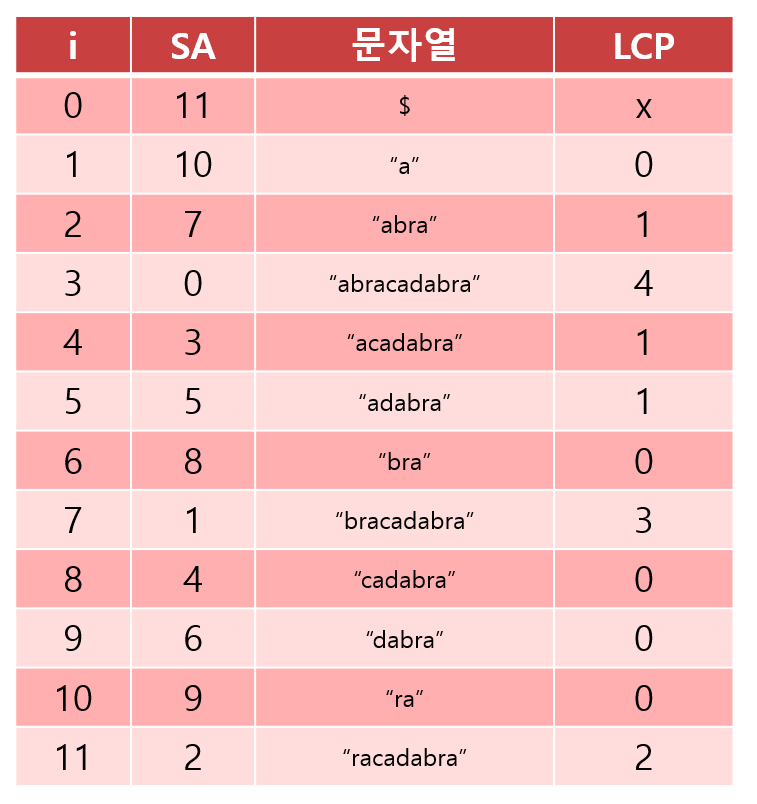
($는 역시 문자열의 끝을 표시하기 위해 임의로 넣은 문자로, 실제로 구현할 때는 넣지 않아도 됩니다)
LCP배열을 나이브하게 구하면 \(O(n^2)\)의 시간이 걸리게 됩니다.
어떻게 빠르게 구할 수 있을까요?
LCP를 Suffix Array에서 순서가 아니라, 원래 인덱스의 순서대로 구하면 빠르게 구할 수 있습니다.

오른쪽의 표를 봅시다.
먼저 맨 첫 접미사인 "abracadabra"는 Suffix Array상에서 이전 문자열과 4글자가 겹칩니다.
그러면 다음 접미사인 "bracadabra"는 앞의 1글자만 없어진 상태이기 때문에, Suffix Array상의 이전 문자열과 3글자 이상이 겹친다는 것이 보장됩니다.
그 이상이 더 겹치는지 여부는 직접 세어주면 됩니다.
위의 방법에서 직접 세었을 때 수가 늘어나는 횟수는 최대 몇 회일까요?
\(S\)의 각 문자들이 최대 1번씩 세어질 수 있기 때문에 최대 \(|S|\)회입니다.
따라서 \(O(n)\)에 LCP배열을 만들 수 있게 됩니다. (\(n = |S|\))
9248번: Suffix Array
Suffix Array란, 문자열 S가 있을 때 그 접미사들을 정렬해 놓은 배열이다. 예를 들어, 문자열 S=banana의 접미사는 아래와 같이 총 6개가 있다. Suffix i banana 1 anana 2 nana 3 ana 4 na 5 a 6 이를 Suffix 순으로 정
www.acmicpc.net
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
|
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
ll gcd(ll a, ll b) { for (; b; a %= b, swap(a, b)); return a; }
string S;
int RA[500001];
int SA[500001];
int tmp[500001];
int LCP[500001];
int main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> S;
for (int i = 0; i < S.size(); i++)
{
RA[i] = S[i]; // 초기 우선순위를 그 문자의 아스키코드로 설정한다.
SA[i] = i;
}
// O(nlog^2n) Suffix Array
for (int k = 1; k < S.size(); k *= 2)
{
auto cmp = [&k](int a, int b)
{
if (RA[a] != RA[b]) return RA[a] < RA[b];
int a2 = a + k < S.size() ? RA[a + k] : -1;
int b2 = b + k < S.size() ? RA[b + k] : -1;
return a2 < b2;
};
sort(SA, SA + S.size(), cmp);
// 두개의 우선순위 페어로 정렬
// 이 부분을 O(n)으로 바꾸면 O(nlogn)이다.
tmp[SA[0]] = 0;
for (int i = 1; i < S.size(); i++)
{
// 각 접미사의 첫 k문자의 우선순위가 같은지 여부 확인
if (!cmp(SA[i - 1], SA[i]) && !cmp(SA[i], SA[i - 1]))
tmp[SA[i]] = tmp[SA[i - 1]];
else
tmp[SA[i]] = tmp[SA[i - 1]] + 1;
}
for (int i = 0; i < S.size(); i++) RA[i] = tmp[i];
}
// 우선순위 배열(RA)을 이용하면 Suffix Array상에서 이전 문자열을 알 수 있다.
int clcp = 0;
for (int i = 0; i < S.size(); i++)
{
if (RA[i] == 0)
{
LCP[RA[i]] = -1;
continue;
}
while (S[i + clcp] == S[SA[RA[i] - 1] + clcp]) clcp++;
LCP[RA[i]] = clcp;
clcp = max(0, clcp - 1);
}
for (int i = 0; i < S.size(); i++) cout << SA[i] + 1 << ' ';
cout << '\n';
for (int i = 0; i < S.size(); i++)
{
if (LCP[i] == -1) cout << "x ";
else cout << LCP[i] << ' ';
}
}
|
이제 Suffix Array와 LCP배열을 이용해 다양한 부분문자열 관련 문제들을 풀 수 있습니다.
제 그룹의 문제집에서 연습 문제들을 관리하고 있습니다.
문제집의 문제들을 보고 싶으시다면, 가입 신청을 해 주세요.
ANZ1217
무슨 내용을 넣어야 좋을까요?
www.acmicpc.net
